Next: 2.3.3 Short-time thermal description: Up: 2.3 Linking different timescales Previous: 2.3.1.1 Nonlinear dynamics Contents
At timescales in the range of pico - nano seconds, the magnetic
response is determined by the characteristic frequency of the
magnetization precession and corresponds to typical ferromagnetic
resonance experiment (FMR) [Slichter 89],
where the small external
perturbation is applied to the systems with the frequency
typically of the order ![]() to
to ![]() . In the theory
of FMR the dynamic Landau-Lifshitz-Gilbert (LLG) equation is
linearized and the solution is being sought as a linear dynamic
response to the small perturbation in terms of the trigonometric
functions proportional to that of the external excitation.
However, at this timescale the system is in a dynamical regime,
and if the external perturbation is not small, it possesses many
characteristics inherent to the dynamics of nonlinear systems.
. In the theory
of FMR the dynamic Landau-Lifshitz-Gilbert (LLG) equation is
linearized and the solution is being sought as a linear dynamic
response to the small perturbation in terms of the trigonometric
functions proportional to that of the external excitation.
However, at this timescale the system is in a dynamical regime,
and if the external perturbation is not small, it possesses many
characteristics inherent to the dynamics of nonlinear systems.
Typical magnetometer measurements of the magnetization response to external fields are on the opposite end of the timescale range. At this scale, the frequency of excitation is much smaller than that of precession frequency or the typical inverse relaxation time, determined by the damping parameter. From the computational point of view, the corresponding response could be calculated in the stationary approximation, i.e. minimizing the total magnetic energy at each external magnetic field value. The intermediate timescale corresponds to that of the adiabatic dynamics in which the dynamical information could be taken on average. In this regime the precession time is faster than the external perturbation, but the relaxation is not fast enough to consider the system as stationary at each point. An example of such dynamics is illustrated in Fig. 2.11. One of the attempts to describe the adiabatic dynamics of single domain particles is due to G. Bertotti et al. [Bertotti 04], who calculated a slow magnetic energy variation in the presence of constant applied field.
![\includegraphics[height=7.cm]{Capitulo2/Graficas2/oleg1}](img311.gif)
|
We study the motion of a single domain particle under an adiabatically varying magnetic field in the small amplitude approximation. The system is the same described in the previous section, but in this case the position of the minimum will also slowly change with time and the equations,
In this case the amplitude of precession ![]() is no more constant. It can be found from
the Eqs. (2.44) and (2.45) in a linear approximation and the
supposition that the applied field is a slow varying function of time,
i.e
is no more constant. It can be found from
the Eqs. (2.44) and (2.45) in a linear approximation and the
supposition that the applied field is a slow varying function of time,
i.e ![]() with
with ![]() .
Consequently,
.
Consequently, ![]() and
and ![]() are also slowly varying
functions of time. The solution for the magnetic moment motion is then:
are also slowly varying
functions of time. The solution for the magnetic moment motion is then:
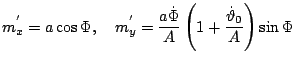
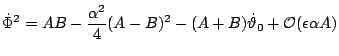
The adiabaticity condition that the variation of the field has to be
less than the ferromagnetic resonance frequency can be rewritten as
![]() . However, the
variable magnetic field
contains two components in the plane and can be dependent
on two adiabatic parameters having
different rates of variation. Therefore, the former
inequality must be complemented by the additional
conditions
. However, the
variable magnetic field
contains two components in the plane and can be dependent
on two adiabatic parameters having
different rates of variation. Therefore, the former
inequality must be complemented by the additional
conditions ![]() ,
,
![]() .
.