In the magnetic recording, the writing process of a bit requires the
application of a field of opposite direction to invert the
magnetization. The recovery of the magnetization after the field pulse
has to last few nano seconds and phenomena as ringing [Crawford 00] are completely
undesired. A realistic simulation of magnetic media needs the inclusion
of the writing head. However, we will include an homogeneous applied
field to the study the dynamical switching, which is by itself an
interesting question. We have simulated an FePt/FeRh thin film under a
constant magnetic field using the LLG equation. The parameters of the
LLG equation are: the damping 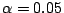 and the integration
time step
and the integration
time step 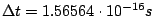 . This time step does not allow
to simulate large system sizes and in this case we have chosen the
in-plane dimensions
. This time step does not allow
to simulate large system sizes and in this case we have chosen the
in-plane dimensions 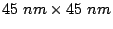 (periodic boundary conditions) and the thicknesses
(periodic boundary conditions) and the thicknesses 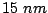 FePt and
FePt and 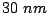 FeRh. The interfacial exchange parameter is
FeRh. The interfacial exchange parameter is
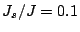 and the anisotropy
and the anisotropy 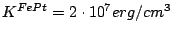 . The field can not take any
value immediately, due to physical limitations, and needs some time to
reach its final value. The field rise time of the pulse was
. The field can not take any
value immediately, due to physical limitations, and needs some time to
reach its final value. The field rise time of the pulse was 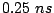 and
the maximum field
and
the maximum field 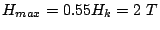 , which
is slightly larger than the corresponding static coercivity for the
film. To compare, the maximum field obtained from the current writing
heads is
, which
is slightly larger than the corresponding static coercivity for the
film. To compare, the maximum field obtained from the current writing
heads is 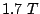 [Kanai 05].
[Kanai 05].
Figure 3.29:
Magnetization profile in an FePt/FeRh film under a field pulse for
different times. The field rise is plotted in the right figure.
![\includegraphics[height=7cm]{Capitulo3/Graficas3/Dinamica}](img584.gif)
|
![\includegraphics[width=\textwidth]{Capitulo3/Graficas3/ramp}](img585.gif) |
Fig. 3.29 represents the temporal
evolution of the magnetization of the film. Before applying the field
the initial state is the remanence, which includes a  domain wall, with the magnetization of the
FePt pointing in the Z positive direction.
The magnetization reversal process is found
to essentially involve domain wall propagation, but is somewhat
complex, and
takes place in three distinct stages. In stage 1 there is a gradual
propagation of the domain wall into the hard FePt phase. During this
stage,
the domain wall slowly changes its nature from
domain wall, with the magnetization of the
FePt pointing in the Z positive direction.
The magnetization reversal process is found
to essentially involve domain wall propagation, but is somewhat
complex, and
takes place in three distinct stages. In stage 1 there is a gradual
propagation of the domain wall into the hard FePt phase. During this
stage,
the domain wall slowly changes its nature from  to
to 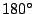 domain wall.
The complete reversal of the FeRh layer, which is equivalent to the
domain wall.
The complete reversal of the FeRh layer, which is equivalent to the 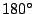 domain wall, is not
necessary to induce
propagation of the domain wall into the FePt phase. During the second
stage
of the magnetization reversal process the magnetization in the FePt
becomes more negative than that in the FeRh. This establishes a
reverse domain wall, which propagates back into the FeRh layer,
resulting in
complete reversal of the whole system. The third stage consists in the
relaxation of the magnetization to its new equilibrium value. In case
the field is removed, this last stage includes the creation of a domain
wall. The duration of this last stage has to be minimized in order to
design a good magnetic recording media.
domain wall, is not
necessary to induce
propagation of the domain wall into the FePt phase. During the second
stage
of the magnetization reversal process the magnetization in the FePt
becomes more negative than that in the FeRh. This establishes a
reverse domain wall, which propagates back into the FeRh layer,
resulting in
complete reversal of the whole system. The third stage consists in the
relaxation of the magnetization to its new equilibrium value. In case
the field is removed, this last stage includes the creation of a domain
wall. The duration of this last stage has to be minimized in order to
design a good magnetic recording media.
Additionally, the soft/hard bilayer presents very interesting
dynamic properties. For example, if for a particular mode or spin-wave
in one
material there are no modes in the coupled material, then the interface
between the two materials acts to pin that particular mode in the first
material, reducing the
amplitude and changing the mode profile. This effect is known as
dynamic pinning [Hoffmann 70]
and can be tuned with an applied field. However, the study of spin
waves in composite media is beyond the scope of this thesis and will be
the focus of future work.
2008-04-04
![\includegraphics[height=7cm]{Capitulo3/Graficas3/Dinamica}](img584.gif)
![\includegraphics[width=\textwidth]{Capitulo3/Graficas3/ramp}](img585.gif)