The single grain of the previous sections is, somehow, an unrealistic
system but can represent isolated grains as those present in patterned
media. In the case of conventional perpendicular recording thin film,
the real sample will be a collection of magnetostatically and
exchangely coupled grains. In previous works on composite media, the
influence of other grains inside the film on a particular grain have
been studied on the bases of an approach similar to the mean-field
approximation [Suess 07].
In order to include the magnetostatic interaction between grains in a
multigrain thin film we have modeled a system of 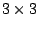 grains with periodic
boundary conditions in X and Y. We have used the model II for the
exchange interactions. The grains are supposed to be exchangely
decoupled
grains with periodic
boundary conditions in X and Y. We have used the model II for the
exchange interactions. The grains are supposed to be exchangely
decoupled  . The energy barrier is calculated
constraining only the hard layer of the central grain and relaxing the
whole system.
. The energy barrier is calculated
constraining only the hard layer of the central grain and relaxing the
whole system.
Figure:
(a) Coercive field, normalized to the anisotropy field (
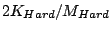 ), and (b) energy barrier as a function of
the interfacial exchange parameters for composite multigrain magnetic
media.
), and (b) energy barrier as a function of
the interfacial exchange parameters for composite multigrain magnetic
media.
|
|
|
|
Figure:
Saddle point and remanence magnetization (minimum) profiles for a
central grain in a multigrain film with 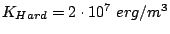 ,
, 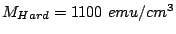 ,
, 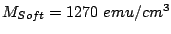 and
and 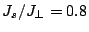 .
.
|
|
Fig. 3.38 shows the energy barrier and the
coercivity as a function of the interfacial exchange in the film. The
coercivity behavior is very similar to that of the single grain (see
Fig. 3.32), but with an
easy-plane anisotropy due to magnetostatics, which results in
additional reduction of coercivity for small interfacial exchange.
Compared with the isolated grain (see Fig. 3.33(b)), the energy
barrier of the grain inside the film is drastically reduced.
Furthermore, the energy barrier value decreases with increasing the
interfacial exchange. The explanation to these facts can be found in
the magnetization distribution shown in Figs. 3.39 and 3.40. The remanent state in the
film is a wall centered at the interface and the saddle point is a wall
centered in the hard grain.
In the ideal case of a infinitely long wire P. Loxley [Loxley 01] derived an expression
for the energy barrier:
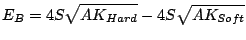 |
(3.10) |
where S is the area of the interface.
To derive this expression the original minimum was considered to be a
domain wall centered in the soft layer.
If the minimum of the system corresponds to the situation when all the
moments are aligned with the easy axis, the energy barrier is 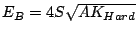 , which
coincides with the case of the domain wall mechanism of the previous
section.
The magnetic configurations that appear in our calculations are
different from these two cases. In our case the domain wall does not
fit into the soft magnetic material and, consequently, the domain wall
in the minimum configuration is centered at the interface. However, Eq.
(3.10) can give an insight into the
physical origin of the reduced energy barrier: the shape anisotropy
originated from the inclusion of the isolated grain in a film leads to
the minimum different from that of the saturated state and reduces the
energy barrier. Due to the dipolar origin of the anisotropy in the
studied case, this reduction is less pronounced for small magnetization
values as seen in Fig. 3.38.
The reduction of the energy barrier with increasing exchange is due to
the fact that the domain wall formation is more effective with more
exchange coupling.
, which
coincides with the case of the domain wall mechanism of the previous
section.
The magnetic configurations that appear in our calculations are
different from these two cases. In our case the domain wall does not
fit into the soft magnetic material and, consequently, the domain wall
in the minimum configuration is centered at the interface. However, Eq.
(3.10) can give an insight into the
physical origin of the reduced energy barrier: the shape anisotropy
originated from the inclusion of the isolated grain in a film leads to
the minimum different from that of the saturated state and reduces the
energy barrier. Due to the dipolar origin of the anisotropy in the
studied case, this reduction is less pronounced for small magnetization
values as seen in Fig. 3.38.
The reduction of the energy barrier with increasing exchange is due to
the fact that the domain wall formation is more effective with more
exchange coupling.
Figure:
Effective energy plot (top left) and corresponding minima (a),(c) and
saddle point (b) for a multigrain composite media with 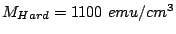 and
and 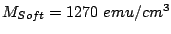 .
.
|
|
In the configurations represented in Fig. 3.40 we can see clearly how the
moments configurations of other grains are affected by the central
grain, due to the magnetostatic interaction. This effect is neglected
in the mean-field approximation implemented in Ref. [Suess 07], which reduces the
applicability of that approach. From Fig. 3.40 we can see that the final
minimum, which is not equivalent to the initial one, is deeper because
this form of flux closure allows more alignment with the easy axis with
the cost of relatively low magnetostatic energy.
The energy barrier reduction is an effect not desirable in magnetic
recording. Possible solutions are a soft material with non-zero
perpendicular anisotropy or a small saturation magnetization value.
These solutions will affect the coercivity reduction of the bilayer.
Figure:
Figure of merit ![$ 2 E_B /[H_c\Sigma _i M_s^iV_i]$](img77.gif) as a function of the
interfacial exchange parameters for composite magnetic media in the
case of: (a) individual magnetic grain and (b) multigrain magnetic
media.
as a function of the
interfacial exchange parameters for composite magnetic media in the
case of: (a) individual magnetic grain and (b) multigrain magnetic
media.
|
|
|
|
2008-04-04
![\includegraphics[width=\textwidth]{Capitulo3/Graficas3/Grafica2.eps}](img619.gif)
![\includegraphics[height=6.5cm]{Capitulo3/Graficas3/domainwallgranular.eps}](img620.gif)
![\includegraphics[width=\textwidth]{Capitulo3/Graficas3/configurationsgrain}](img623.gif)