The modeling of the surface anisotropy contribution is a complex field of research. Néel proposed a phenomenological model of the surface anisotropy called after that the "Néel surface anisotropy (NSA) model". The model assumes an origin of the anisotropy basing on the lack of the atomic bonds on the surface of a crystal. The surface anisotropy contribution is described as a pair-interaction of spins in the following way:
Here 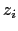 is the number of nearest neighbors of the surface spin i, (known as the coordination number),
is the number of nearest neighbors of the surface spin i, (known as the coordination number),
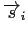 is a unit vector pointing along the magnetization direction,
is a unit vector pointing along the magnetization direction, is the distance between spin i and j,
is the distance between spin i and j,
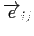 is the unit vector connecting the spin i to its nearest neighbor j, the factor
is the unit vector connecting the spin i to its nearest neighbor j, the factor 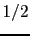 is added in order not to count twice the pair interaction and
is added in order not to count twice the pair interaction and 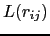 is the pair-anisotropy coupling constant, also called the Néel surface anisotropy constant, which depends on the distance between spins [47], see Fig. 1.3.
is the pair-anisotropy coupling constant, also called the Néel surface anisotropy constant, which depends on the distance between spins [47], see Fig. 1.3.
If 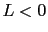 the surface anisotropy is locally in-plane and is out-of-plane if
the surface anisotropy is locally in-plane and is out-of-plane if 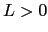 . L depends on the interatomic distance
. L depends on the interatomic distance  (in the following we will omit the subindex i and j) according to the expression:
(in the following we will omit the subindex i and j) according to the expression:
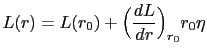 |
(9) |
where 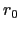 is the unstrained bond length and
is the unstrained bond length and  is the bond strain.
is the bond strain.
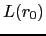 and
and
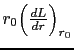 depend on the magnetostriction and elastic constants, therefore
depend on the magnetostriction and elastic constants, therefore 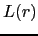 also depends on these magnitudes.
All these relations make obvious that the NSA depends on the orientation of the local magnetization with respect to the surface, the orientation of the surface with respect to the crystalline axes, and the loss of neighbors. This way, atoms located at different positions at the surface can possess a different surface anisotropy value. For example, in Fig. 1.4 (from Ref. [14]) we show the neighborhood of atoms located at different positions in a truncated octahedral nanoparticle, which have different directions of the local easy axes and strengths of the surface anisotropy [14].
also depends on these magnitudes.
All these relations make obvious that the NSA depends on the orientation of the local magnetization with respect to the surface, the orientation of the surface with respect to the crystalline axes, and the loss of neighbors. This way, atoms located at different positions at the surface can possess a different surface anisotropy value. For example, in Fig. 1.4 (from Ref. [14]) we show the neighborhood of atoms located at different positions in a truncated octahedral nanoparticle, which have different directions of the local easy axes and strengths of the surface anisotropy [14].
Figure 1.4:
The different environment of the atoms in a fcc octahedral nano-particle ( from Ref. [14]).
|
|
Within this model the magnetic surface anisotropy of a given atom can be calculated summing pair-interactions with its nearest neighbors. Despite the fact that this model provides an adequate description of the symmetry of the surface magnetic anisotropy it doesn't provide a physical understanding of its origin since it has a phenomenological character. With the aim to go deeper in the physical origin of the magnetic surface anisotropy we have to consider the effects of the spin-orbit coupling and the ligand field.
Rocio Yanes
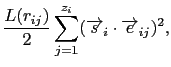
![]() the surface anisotropy is locally in-plane and is out-of-plane if
the surface anisotropy is locally in-plane and is out-of-plane if ![]() . L depends on the interatomic distance
. L depends on the interatomic distance ![]() (in the following we will omit the subindex i and j) according to the expression:
(in the following we will omit the subindex i and j) according to the expression:
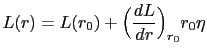
![]() and
and
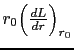 depend on the magnetostriction and elastic constants, therefore
depend on the magnetostriction and elastic constants, therefore ![]() also depends on these magnitudes.
All these relations make obvious that the NSA depends on the orientation of the local magnetization with respect to the surface, the orientation of the surface with respect to the crystalline axes, and the loss of neighbors. This way, atoms located at different positions at the surface can possess a different surface anisotropy value. For example, in Fig. 1.4 (from Ref. [14]) we show the neighborhood of atoms located at different positions in a truncated octahedral nanoparticle, which have different directions of the local easy axes and strengths of the surface anisotropy [14].
also depends on these magnitudes.
All these relations make obvious that the NSA depends on the orientation of the local magnetization with respect to the surface, the orientation of the surface with respect to the crystalline axes, and the loss of neighbors. This way, atoms located at different positions at the surface can possess a different surface anisotropy value. For example, in Fig. 1.4 (from Ref. [14]) we show the neighborhood of atoms located at different positions in a truncated octahedral nanoparticle, which have different directions of the local easy axes and strengths of the surface anisotropy [14].
![\includegraphics[totalheight=0.4\textheight]{Surf_Arreng_JametPRB04.eps}](img199.gif)