1 Motivation

How long the magnetization can remain fixed in a determinate direction is one of the key questions in magnetism, or equivalently the determination of the stability of a magnetic system. It is worth pointing out here that any discussion of magnetic stability will involve evaluation of the energy barrier separating the two magnetic states, because this controls the energy required to change magnetic moment of a system from one direction to another by means of thermal activation. The probability of the switching of the magnetization is related to the energy barrier through the Arrhenius-Néel law [53].

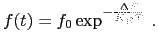$$f(t)=f_{0}\exp^{-\frac{\Delta E}{K_{B}T}} .$$ (43)

Here the prefactor $f_{0}$ is the attempt frequency, $\Delta E$ is the energy barrier, $K_{B}$ is the Boltzmann constant, and T is the temperature of the system.

Experimentally the relevant energy barrier $\Delta E$ may be extracted from the measurement of the blocking temperature $T_{B}$. It has been widely reported that the surface effects can modify the energy barrier through a modification of the "effective anisotropy", $\mathcal{K}^{eff}$ [36,9,20,14,32]. The effective anisotropy constant simply may be defined through the energy barrier as:

$$\mathcal{K}^{eff}=\Delta E/V,$$ (44)

where V is the volume of the nanoparticle. In the case of magnetic nanoparticle modeled by a macro-spin approximation with bulk uniaxial or cubic magnetocrystalline anisotropy, the energy barrier has the following dependence on the core anisotropy constant ($K_{c}$), defined here as a macroscopic anisotropy energy density:

$$\Delta E/V=\left\{\begin{array}{ccc} K_{c} & \textrm{uniaxial ani... ...id K_{c}\mid}{12} & \textrm{cubic anisotropy with} & K_{c}<0 \end{array}\right.$$ (45)

Therefore, the analysis of the energy potential is unavoidable since it is a crucial step in calculating relaxation rates and thereby in the study of the magnetization stability against thermal-activated reversal.