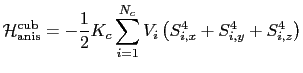1 Atomistic model
We consider a magnetic system of  spins in the classical
many-spin approach, i.e., taking account of its intrinsic
properties such as the lattice structure and system size.
The magnetic properties of such system are described by the anisotropic
Heisenberg model for classical
spins
spins in the classical
many-spin approach, i.e., taking account of its intrinsic
properties such as the lattice structure and system size.
The magnetic properties of such system are described by the anisotropic
Heisenberg model for classical
spins  (with
(with  ). The
Hamiltonian includes the (nearest-neighbor) exchange interactions,
single-site bulk (
). The
Hamiltonian includes the (nearest-neighbor) exchange interactions,
single-site bulk (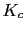 ) and
Néel
surface anisotropy (
) and
Néel
surface anisotropy (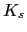 ):
):
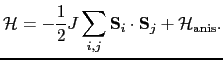 |
(53) |
where J is the exchange parameter.
The anisotropy energy  will be
different if we are working with bulk spins or surface spins. For bulk
spins, i.e., those spins with full coordination, the
anisotropy energy
will be
different if we are working with bulk spins or surface spins. For bulk
spins, i.e., those spins with full coordination, the
anisotropy energy 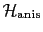 is taken
either as
uniaxial with easy axis along
is taken
either as
uniaxial with easy axis along 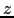 and anisotropy constant
and anisotropy constant 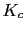 (per
atomic volume), that is
(per
atomic volume), that is
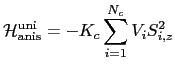 |
(54) |
or cubic,
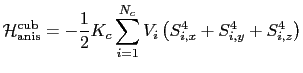 |
(55) |
where 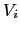 is the volume
of the atomic atom i,
is the volume
of the atomic atom i, 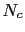 is the number of bulk spins in the thin film.
For surface spins the anisotropy is taken according to the
Néel's
model, expressed as:
is the number of bulk spins in the thin film.
For surface spins the anisotropy is taken according to the
Néel's
model, expressed as:
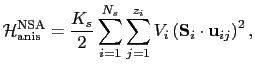 |
(56) |
where 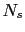 is the number of surface
spins,
is the number of surface
spins, 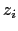 the number of
nearest neighbors of site
the number of
nearest neighbors of site 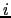 ,
and
,
and 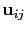 a unit vector
connecting this site to its nearest neighbors labeled by
a unit vector
connecting this site to its nearest neighbors labeled by  .
.
The magnetic systems modeled in this chapter are thin films. The
magnetic parameters of the system under study are presented in table 4.1.
Rocio Yanes
![]() will be
different if we are working with bulk spins or surface spins. For bulk
spins, i.e., those spins with full coordination, the
anisotropy energy
will be
different if we are working with bulk spins or surface spins. For bulk
spins, i.e., those spins with full coordination, the
anisotropy energy ![]() is taken
either as
uniaxial with easy axis along
is taken
either as
uniaxial with easy axis along ![]() and anisotropy constant
and anisotropy constant ![]() (per
atomic volume), that is
(per
atomic volume), that is