3 Modeling the effect of the anisotropy re-orientation due to the surface effects
In many cases the direction of the easy axes in the system suffers a change due to the existence of the surface effects [136,137].
Such effect can occur when the easy directions of the surface and
bulk anisotropies compete, see Fig. 4.16. The temperature re-orientation of the easy axis in magnetic thin films has previously been refereed in a huge number of papers [56,138,119,63,117,118,54,120].
Figure 4.16:
(Left) System Geometry of a thin film with 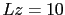 with a sc crystalline structure. Uniaxial anisotropies with easy axis in the bulk and on the surface are depicted on the right side (perpendicular to each other).
with a sc crystalline structure. Uniaxial anisotropies with easy axis in the bulk and on the surface are depicted on the right side (perpendicular to each other).
![\includegraphics[totalheight=0.15\textheight]{LD_sc_surf.eps}](img671.gif)
![\includegraphics[totalheight=0.1\textheight]{Unix_KsZ.eps}](img688.gif) |
Figure 4.17:
The system torque evaluated for thin film with 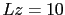 , uniaxial anisotropy in the bulk and Néel Surface anisotropy
, uniaxial anisotropy in the bulk and Néel Surface anisotropy
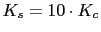 , sketched in Fig. 4.16. The bulk easy axis is parallel to X axis. (Left graphic) Curve of the component Y of the total torque as a function of
, sketched in Fig. 4.16. The bulk easy axis is parallel to X axis. (Left graphic) Curve of the component Y of the total torque as a function of 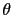 angle for several temperatures
angle for several temperatures
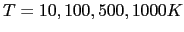 . (Right graphic)
Total, surface and bulk torques at
. (Right graphic)
Total, surface and bulk torques at 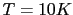 .
.
![\includegraphics[totalheight=0.27\textheight]{LD_sc_ex_TorTemp.eps}](img689.gif)
![\includegraphics[totalheight=0.27\textheight]{LD_sc_ex_TSC.eps}](img690.gif) |
We first analyze the existence of the re-orientation transition in magnetic thin films as a function of the temperature.
As it can be seen in Fig. 4.17 (right) (thin film with 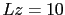 ), in the case of perpendicular configuration of the easy axes the surface, the torque also follows the
), in the case of perpendicular configuration of the easy axes the surface, the torque also follows the
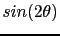 behavior and the effective surface anisotropy could be extracted. The sign of the effective surface anisotropy constant obtained by fitting of the surface restoring torque curve is opposite to the bulk one, it indicates the different orientations of easy axis in the bulk which easy axis geometry of Fig. 4.16.
behavior and the effective surface anisotropy could be extracted. The sign of the effective surface anisotropy constant obtained by fitting of the surface restoring torque curve is opposite to the bulk one, it indicates the different orientations of easy axis in the bulk which easy axis geometry of Fig. 4.16.
Figure 4.18:
Temperature dependence of the effective anisotropy constant for different thin film thicknesses.
|
|
In this system at low temperatures the magnetization lies along the surface easy
direction, perpendicular to the plane.
As the temperature is increased the surface contribution to the anisotropy
energy rapidly decreases, so that the system magnetization is re-orientated along the
bulk easy direction, i.e. in the plane. This is illustrated in Fig. 4.17 (left), where we plot the Y component of the total torque acting on
the same thin film at different temperatures. As it can be seen, at low temperatures the positions of the maximum of the torque corresponds to that of the uniaxial out-of-plane anisotropy while at high temperatures the situation corresponds to that of the in-plane anisotropy.
Figure:
Temperature dependence of effective anisotropy
for a thin film with competing surface (easy plane) and bulk (parallel to Z axis)
anisotropies for different magnitudes of
 .
.
|
|
Next we analyze the existence of the re-orientation transition in magnetic thin films as a function of their thickness. We increase the thickness from 5 to 15 atomic layer. The temperature dependence of the effective anisotropy is plotted in Fig. 4.18.
In ultra-thin films the total anisotropy of the system is governed by the surface anisotropy up to the Curie temperature. If the thickness of the thin film is large, then the total anisotropy is dominated by the bulk anisotropy and the easy axis is parallel to bulk one.The re-orientation transition occurs in a intermediate region of thickness and the re-orientation temperature depends on the thin film thickness.
One interesting property of the temperature dependent re-orientation
transition is that, depending on the choice of non-magnetic interface
material, the temperature of the transition can be tuned.
To illustrate this phenomenon, Fig 4.19 shows a plot
of the temperature dependence of the total anisotropy for different
Néel anisotropy constants, emulating the effect of changing the coating of the material. Note that in this case the easy axis of the surface anisotropy is in-plane and the bulk anisotropy is assumed to be perpendicular to the plane (as in coated materials for perpendicular magnetic recording applications).
Rocio Yanes
![\includegraphics[totalheight=0.15\textheight]{LD_sc_surf.eps}](img671.gif)
![\includegraphics[totalheight=0.1\textheight]{Unix_KsZ.eps}](img688.gif)
![\includegraphics[totalheight=0.27\textheight]{LD_sc_ex_TorTemp.eps}](img689.gif)
![\includegraphics[totalheight=0.27\textheight]{LD_sc_ex_TSC.eps}](img690.gif)
![\includegraphics[totalheight=0.35\textheight]{LD_sc_ex_Keff_diffLz.eps}](img692.gif)
![\includegraphics[
totalheight=0.3\textheight]{cmc_thin_film.eps}](img694.gif)