Next: 1 Temperature dependence of Up: 5 Temperature dependence of Previous: 1 Introduction Contents
To evaluate the temperature dependence of the macroscopic anisotropy constant we use the constrained Monte Carlo method (CMC) introduced in the section 4.2 of the previous chapter. The CMC is an algorithm of the Monte Carlo type which allows to include both thermodynamic fluctuations and entropy into the evaluation of macroscopic quantities such as the temperature dependent magnetic anisotropy. Differently to chapter 2, the internal energy in this case is substituted by the free energy
![]() . We retrieve the anisotropy constants by calculating the average restoring torque in the equilibrium as a function of the constrained magnetization direction
. We retrieve the anisotropy constants by calculating the average restoring torque in the equilibrium as a function of the constrained magnetization direction
![]() , where
, where
![]() are the constrained polar and azimuthal angles.
are the constrained polar and azimuthal angles.
![]() .
.
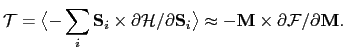 |
(76) |