Next: 2.2.3.2 Magnetostatic potential. The Up: 2.2.3 Micromagnetics: classical approach Previous: 2.2.3 Micromagnetics: classical approach Contents
The process of demagnetization in a standard hysteresis experiment
consists basically of a series of stationary states. The time of
measurement (typically miliseconds) is as large as to disregard
rapid dynamic effects (occurring at pico - nanoseconds). For this
kind of process the micromagnetic approach, firstly introduced by
W.F. Brown [Brown 63a], is used. The micromagnetism is a
semiclassical approach that considers the magnetization
![]() as a vector function of the spatial coordinates, but
with constant module
as a vector function of the spatial coordinates, but
with constant module ![]() . This implies a continuous approximation
that ignores any discrete effect. The magnitude
. This implies a continuous approximation
that ignores any discrete effect. The magnitude ![]() is the
saturation magnetization and it is defined as the density of
magnetic moments (per unit of volume in the material). It is more
useful to work with the magnetization unit vector
is the
saturation magnetization and it is defined as the density of
magnetic moments (per unit of volume in the material). It is more
useful to work with the magnetization unit vector
![]() . The energies appearing in the
atomistic level are substituted by a functional of
. The energies appearing in the
atomistic level are substituted by a functional of
![]() :
:
The micromagnetic exchange energy is a continuous version of the atomistic exchange. The expression is the square of a derivative and, therefore, the minimum value corresponds to the saturated stated. Therefore, the micromagnetic exchange also favors all the moments to be parallel. For granular magnetic material the exchange constant is often phenomenological.
The atomistic magnetic moment and the saturation magnetization are related through
The magnetization state is found by minimizing the total energy with
respect to the function
![]() . Namely, we must solve
. Namely, we must solve
![]() with the restriction
with the restriction
![]() . The minimum found by this procedure is
normally a relative minimum of the total energy. The minimization
procedure depends on the initial conditions and the final state is
dependent of the initial state. On the other hand, this is also the
case in the experiments. The variational problem solution satisfies
. The minimum found by this procedure is
normally a relative minimum of the total energy. The minimization
procedure depends on the initial conditions and the final state is
dependent of the initial state. On the other hand, this is also the
case in the experiments. The variational problem solution satisfies
![]() =0 with the addition of a
Lagrange multiplier term, proportional to
=0 with the addition of a
Lagrange multiplier term, proportional to
![]() .
Therefore, the solution of variational problem also satisfies the
Brown condition for minimum:
.
Therefore, the solution of variational problem also satisfies the
Brown condition for minimum:
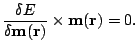
From Eq. (2.8) the total effective field is a sum of exchange, anisotropy, external and magnetostatic fields:
Until the rapid development of the computers, the micromagnetics was
an analytical theory and many analytical results were derived.
However, normally all of them are based on simplifications and have
very limited regions of applicability. In numerical approaches we
divide or discretize the sample by the discretization length
![]() , considering a constant magnetization inside each element.
, considering a constant magnetization inside each element.
There are two physically relevant parameters that we need to take in
account in order to select the size of the discretization length
![]() : the wall-width parameter
: the wall-width parameter
In the literature there are two main methods of discretization: Finite Differences (FD) [Berkov 93] and Finite Elements Method (FEM) [Fidler 00]. The advantage of the finite differences method is its easy implementation but its main disadvantage is its inability to describe irregular shapes. To overcome this problem Gibbons proposed the Embedded Curved Boundary (ECB) method as an alternative based on the interpolation of the boundary elements [Gibbons 00]. For curved surfaces FEM is best suited because its elements are tetrahedra with variable size , although any numerical approach will fail to describe real surfaces. At the present, there are several software packages available for micromagnetic simulations. Most of them are commercial programs, but also there have been efforts to release free source codes in particular Oommf [OOMMF ], which uses FD method with Fast Fourier Transform, and magpar [Magpar ], which uses FEM simulations. In our calculations in the following chapters we used codes developed inside the group that use the finite differences method.
In the numerical solution of Eq. (2.16) the right term can never be zero due to numerical convergence problem. We want this value to be as low as possible, but in practice we finish our calculation when a tolerance value has been reached. In our calculation we use the following definition for the micromagnetic error:
Finally, we will return to the micromagnetic exchange constant ![]() .
Its relation with the atomistic exchange parameter can be easy
calculated if we compare the finite difference version of Eq.
(2.18) and the effective field arising from
Eq. (2.5) and making
.
Its relation with the atomistic exchange parameter can be easy
calculated if we compare the finite difference version of Eq.
(2.18) and the effective field arising from
Eq. (2.5) and making ![]() equal to the lattice
distance. Thus in a tetragonal with lattice size parameters
equal to the lattice
distance. Thus in a tetragonal with lattice size parameters
![]() and
and
![]() :
:
2008-04-04