Figure:
Simulated coercivity as a function of the angle of the applied field 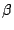 for particles with
dimensions: (a)
for particles with
dimensions: (a) 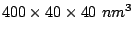 and (b)
and (b) 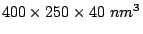 .
.
|
|
|
|
One of the largest possible differences between experimental situation
and the model is the misalignment between the particle axis and the
applied field. To include this into consideration,
we first have calculated the angular dependence of the demagnetization
process, applying the field with an angle 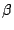 with respect to the long axis of the
particles. We can again distinguish two types of behavior as shown in
Fig. 4.10. In the small aspect ratio case
the angular dependence of the coercivity is proper to the biaxial
anisotropy.
For the particles with smaller widths the angular coercivity is
determined by the strong shape anisotropy and the characteristics of
the moment configurations corresponding to the remanence do not depend
on the saturating field orientation for
with respect to the long axis of the
particles. We can again distinguish two types of behavior as shown in
Fig. 4.10. In the small aspect ratio case
the angular dependence of the coercivity is proper to the biaxial
anisotropy.
For the particles with smaller widths the angular coercivity is
determined by the strong shape anisotropy and the characteristics of
the moment configurations corresponding to the remanence do not depend
on the saturating field orientation for  .
Differently from this, in the case
.
Differently from this, in the case 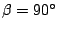 both the
remanence configuration and the reversal process occurred through
moment configurations clearly different from those previously
discussed, see Fig 4.11. The configuration
at the remanence corresponded to the disappearance of the
close-to-uniform moment configuration observed at the particle core
which is substituted by the two Néel-like walls with a cross-tie
domain wall between them.
both the
remanence configuration and the reversal process occurred through
moment configurations clearly different from those previously
discussed, see Fig 4.11. The configuration
at the remanence corresponded to the disappearance of the
close-to-uniform moment configuration observed at the particle core
which is substituted by the two Néel-like walls with a cross-tie
domain wall between them.
Figure:
Remanence configuration of 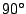 hysteresis loop for the
hysteresis loop for the 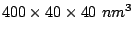 particle.
particle.
|
|
Figure 4.12:
Ribbon width dependence of the coercivity of a set of
non-interacting ribbons having distributed orientations.
|
|
Finally, we evaluated the influence on the model system
coercivity of the occurrence of misalignment
between the orientations of the nanoribbons, present in the
measured samples. In Fig. 4.12 we plot the
calculated
ribbon coercivity as a function of their widths for a non-interacting
set of ribbons. We
assumed the geometrical orientations, distributed according to a
Gaussian distribution centered at  or
or 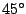 with the
direction of the applied field and having a width
with the
direction of the applied field and having a width 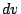 . The result is the convolution of the
gaussian distribution with the corresponding coercivity as a function
of the angle. As it is possible to observe from the Figure,
the consideration of ribbon misorientation reduces, with respect
to the absence of it, the differences between the experimental and
the simulational results.
. The result is the convolution of the
gaussian distribution with the corresponding coercivity as a function
of the angle. As it is possible to observe from the Figure,
the consideration of ribbon misorientation reduces, with respect
to the absence of it, the differences between the experimental and
the simulational results.
2008-04-04
![\includegraphics[width=\textwidth]{Capitulo4/Graficas4/angular.eps}](img677.gif)
![\includegraphics[height=7.cm]{Capitulo4/Graficas4/textura.eps}](img681.gif)
![]() or
or ![]() with the
direction of the applied field and having a width
with the
direction of the applied field and having a width ![]() . The result is the convolution of the
gaussian distribution with the corresponding coercivity as a function
of the angle. As it is possible to observe from the Figure,
the consideration of ribbon misorientation reduces, with respect
to the absence of it, the differences between the experimental and
the simulational results.
. The result is the convolution of the
gaussian distribution with the corresponding coercivity as a function
of the angle. As it is possible to observe from the Figure,
the consideration of ribbon misorientation reduces, with respect
to the absence of it, the differences between the experimental and
the simulational results.