Next: 4.4 Angular dependence of Up: 4. Magnetization reversal in Previous: 4.2 Simulational model Contents
Fig. 4.5 presents the results obtained from our simulation for the hysteresis cycles of ribbons having different widths and bulk biaxial magnetocrystalline anisotropy exclusively. The magnetic moment configuration (see Figs. 4.6 and 4.8) occurring during these processes allowed us to identify two different reversal modes associated to the particles having large and small aspect ratio, respectively.
An initial result, observed at all the applied field values and in
all
the simulated particles, was the fact that the orientation of the
magnetic moments did not depend on the position along the system
thickness. That result could be ``a priori'' expected from the
particle thickness value which was below the Fe exchange correlation
length, ![]() . Thus, in
the following we will discuss all the moment
configurations present in the modeled systems in terms of 2D moment
distributions corresponding to planes parallel to the two largest
dimensions of the particles.
. Thus, in
the following we will discuss all the moment
configurations present in the modeled systems in terms of 2D moment
distributions corresponding to planes parallel to the two largest
dimensions of the particles.
![\includegraphics[width=\textwidth]{Capitulo4/Graficas4/procesodelgada}](img655.gif)
|
In the case of the particles having the largest aspect ratios (see
the complete reversal sequence in Fig. 4.6,
where data
corresponding to the particle having ![]() are
presented) the remanent state corresponded to the well known
``S-type'' configuration, which only differs from the single domain one
in the quasi-parallel-to-the-surface moment structures present at
the particle ends. Those structures are a result of the minimization
of the magnetostatic energy and their presence results in the
spreading
of the magnetic poles that should
be localized at the particle surfaces in the case of the uniform
magnetization configuration. The ``S-type'' configuration evolves with
the increase
of the demagnetizing field to the formation of closure-like domains
at both ends of the particle and finally to a collective
irreversible rotation which leads to a ``S-type'' state symmetric to
that corresponding to the magnetizing field remanence. The hysteresis
loops presented in Fig. 4.5 evidence
that the coercive force decreases
with the decrease of the aspect ratio value see (Fig. 4.7).
are
presented) the remanent state corresponded to the well known
``S-type'' configuration, which only differs from the single domain one
in the quasi-parallel-to-the-surface moment structures present at
the particle ends. Those structures are a result of the minimization
of the magnetostatic energy and their presence results in the
spreading
of the magnetic poles that should
be localized at the particle surfaces in the case of the uniform
magnetization configuration. The ``S-type'' configuration evolves with
the increase
of the demagnetizing field to the formation of closure-like domains
at both ends of the particle and finally to a collective
irreversible rotation which leads to a ``S-type'' state symmetric to
that corresponding to the magnetizing field remanence. The hysteresis
loops presented in Fig. 4.5 evidence
that the coercive force decreases
with the decrease of the aspect ratio value see (Fig. 4.7).
![\includegraphics[height=7.cm]{Capitulo4/Graficas4/biaxialcoerc}](img657.gif)
|
The field at which the reversal occurs can be compared to the
classical shape anisotropy field associated to the particle
dimensions. For that purpose we can consider the demagnetizing field
model for thin films discussed in [O'Handley 00,
Pages 42-43]. If
the dimensions of the system are ![]() (width)
(width) ![]() (height)
(height) ![]() (thickness), then the demagnetizing
factors,
(thickness), then the demagnetizing
factors, ![]() and
and ![]() , associated to the
two larger dimensions
are in SI units:
, associated to the
two larger dimensions
are in SI units:
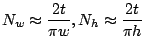 |
(4.1) |
| (4.2) |
In the case of the particle having the larger aspect ratio, ![]() ,
, ![]() , and
, and ![]() , this results in a
shape anisotropy field of
, this results in a
shape anisotropy field of ![]() , which is
significantly larger than our simulational
result for the coercive force (
, which is
significantly larger than our simulational
result for the coercive force (
![]() ). This
fact is related to
the moment configurations obtained from our micromagnetic
simulations at the remanence and, more concretely, to the
inhomogeneous moment structures present at the ends of the
particles.
). This
fact is related to
the moment configurations obtained from our micromagnetic
simulations at the remanence and, more concretely, to the
inhomogeneous moment structures present at the ends of the
particles.
In the case of the particles having smaller aspect ratios, both the
reversal mode and the associated moment configurations are more
complex than those previously discussed. At the saturation remanence
(see Fig. 4.8(a)), the moments at a
layer close to the
surface of the particles point essentially parallel to that surface,
whereas those at the inner core of the particles are oriented along
the direction of one of the magnetocrystalline (100) easy axes. The
transition from the ``S-type'' configuration characteristic of the
elongated particles to that present in the small aspect ratio ones
is illustrated in Fig. 4.9 in which we have
plotted
the evolution with the aspect ratio of the orientation of the moment
present
at the center of the system. These data allow to know that only for
particle widths above ![]() the inner moments point parallel to the
magnetocrystalline easy axis.
the inner moments point parallel to the
magnetocrystalline easy axis.
![\includegraphics[width=0.7\textwidth]{Capitulo4/Graficas4/procesoancha}](img672.gif)
|
![\includegraphics[height=7.cm]{Capitulo4/Graficas4/degrees}](img673.gif)
|
The next steps of the magnetization reversal of these small aspect
ratio particles are shown in Fig. 4.8.
From this figure
it is possible to see how the first partially reversed region is the
particle core which moments rotate irreversibly from their direction
at the remanence to that of the closest easy axis forming the
smallest angle with the applied demagnetizing field. For a field
slightly below that corresponding to this rotation the particle
exhibits uniform magnetization domains separated by charged 45º
walls. Since for the particles having small aspect ratio most of the
volume
of the particle corresponds to the core moments their reversal
governs the coercive force value (evaluated from the ![]() condition).
condition).
It is interesting to point out that the field corresponding to the particle core reversal approaches for sufficiently small aspect ratios the value corresponding to the Stoner-Wohlfarth (SW) model discussed in Section 5.3.2 (see Fig. 4.7 where we show the width dependence of the core reversal field and the corresponding SW field). Thus, for these conditions the surface layer minimizes the stray fields linked to the finite size of the particles and, very interestingly, the system behaves globally as an infinite one, reversing through a coherent rotation mechanism.
Once the particle core experiences the low field irreversible
rotation their moments rotate reversibly towards the field
direction. In the large width particles and for a field just above
that corresponding to the rotation, the wall-like structure allowing
the transition from the core moments direction to the orientation of
the moments in the long axis uniform magnetization surface layer,
sweeps an angle of ca. ![]() .
Further reorientation of the core
moments towards the applied field reduces both the swept angle and
the width of this wall. The reversal process is completed by the
annihilation of the core-surface wall. This process occurs at a
field approximately independent from the sample size and through the
irreversible rotation of the surface moments. Immediately after that
annihilation the system moment configuration is of the ``S-type''.
.
Further reorientation of the core
moments towards the applied field reduces both the swept angle and
the width of this wall. The reversal process is completed by the
annihilation of the core-surface wall. This process occurs at a
field approximately independent from the sample size and through the
irreversible rotation of the surface moments. Immediately after that
annihilation the system moment configuration is of the ``S-type''.
The efficiency of the surface structures to minimize the magnetostatic energy contribution is also relevant from the point of view of the analysis of the interparticle dipolar interactions that should here be largely reduced in comparison to a case in which the surface moment structures were absent. However, it is not clear that the pole avoidance is the best way to minimize the total energy of the many particles. An efficient compensation of charges in neighboring particles can be more advantageous than their avoidance.
Finally, in Fig. 4.7 is plotted,
for comparison, the simulational and experimental coercivity. Whereas
for reduced widths the simulational results
are up to two times larger than the experimental ones (which is in
principle plausible due
to the absence in the model of different types of defects, i.e.:
morphological, associated
to reduced crystallinity regions, etc., that could help to reduce the
coercivity) for widths
larger than ca. ![]() the experimental data are slightly larger than the simulational ones,
clearly suggesting that mechanisms different from the presence of the
mentioned defects
should account for the differences between the experimental and the
simulational data.
Note also that in experimental situations the irreversible jumps of the
hysteresis cycles
are normally smoothed due to slight distribution of geometrical and
magnetic parameters
between different objects.
the experimental data are slightly larger than the simulational ones,
clearly suggesting that mechanisms different from the presence of the
mentioned defects
should account for the differences between the experimental and the
simulational data.
Note also that in experimental situations the irreversible jumps of the
hysteresis cycles
are normally smoothed due to slight distribution of geometrical and
magnetic parameters
between different objects.