5.3.2 Coherent Reversal Model
Figure 5.14:
Angular dependence of the switching field for the coherent
rotation model.
|
|
As a first approach we can use a simple model of an Fe film to
compare with the results in the lithographed film. This simple model
is equivalent to the Stoner-Wohlfarth model for uniaxial anisotropy
particles, replacing the uniaxial anisotropy with the Fe twofold
anisotropy.
We consider only in-plane magnetization and do not allow in-plane
magnetization variations, so that coherent reversal is supposed. As a
consequence the energy can be expressed as a function of a single
coordinate 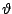 ,
the angle between the magnetization and the
applied field direction:
,
the angle between the magnetization and the
applied field direction:
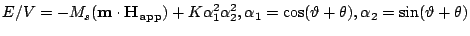 |
(5.1) |
where 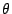 is the
angle between the easy axis and the applied field direction.
The magnetization will evolve through a reversible rotation, until
the state of the magnetization becomes an inflexion point of the energy
function and another
solution branch becomes the minimum. We can only find analytic solution
in
the case of applied field in the direction of the easy axis or the hard
axis. For an easy or hard axis loop the energy derivative becomes:
is the
angle between the easy axis and the applied field direction.
The magnetization will evolve through a reversible rotation, until
the state of the magnetization becomes an inflexion point of the energy
function and another
solution branch becomes the minimum. We can only find analytic solution
in
the case of applied field in the direction of the easy axis or the hard
axis. For an easy or hard axis loop the energy derivative becomes:
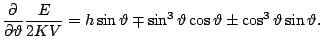 |
(5.2) |
The hysteresis loop can be calculated verifying the stability of
the zeroes of Eq. (5.2). The rest of the
cases have
to be solved numerically.
Figure 5.15:
Hysteresis loops for the coherent rotation model of biaxial
anisotropy for the applied field in (a) the easy axis direction and (b)
the hard axis direction. In the easy axis plot
the applied field values for which an alternative minimum exists and
the corresponding magnetization are shown.
|
|
In Fig. 5.14 we show the dependence of the
magnetization jumps on the angle 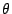 . The model predicts two
jumps for angles larger than a critical value
. The model predicts two
jumps for angles larger than a critical value 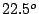 , except for the hard axis configuration in
which
only one jump appears. The existence of two jumps is the consequence
of the biaxial anisotropy. When the minimum opposite to the field
direction becomes unstable an intermediate minimum still exists that
does not correspond to the alignment with field. In fact the system
finds the next relative minimum along the angle
, except for the hard axis configuration in
which
only one jump appears. The existence of two jumps is the consequence
of the biaxial anisotropy. When the minimum opposite to the field
direction becomes unstable an intermediate minimum still exists that
does not correspond to the alignment with field. In fact the system
finds the next relative minimum along the angle 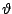 but not the
absolute minimum. The second jump will occur when this intermediate
minimum becomes also unstable. In Fig. 5.15(a)
the
alternative minimum is shown for an easy axis loop. This minimum does
not exist when the branch corresponding to the magnetization
saturated along the positive direction is unstable and, therefore, the
magnetization will never be in such state during hysteresis
processes.
The model predicts the occurrence of two coercive fields, observed
experimentally. However, in the experimental situation such fields
existed for all applied field angles. Clearly, the model does not
include the possibility of inhomogeneous magnetization reversal.
2008-04-04
but not the
absolute minimum. The second jump will occur when this intermediate
minimum becomes also unstable. In Fig. 5.15(a)
the
alternative minimum is shown for an easy axis loop. This minimum does
not exist when the branch corresponding to the magnetization
saturated along the positive direction is unstable and, therefore, the
magnetization will never be in such state during hysteresis
processes.
The model predicts the occurrence of two coercive fields, observed
experimentally. However, in the experimental situation such fields
existed for all applied field angles. Clearly, the model does not
include the possibility of inhomogeneous magnetization reversal.
2008-04-04
![\includegraphics[height=5.25cm]{Capitulo5/Graficas5/loopstonea}](img750.gif)
![\includegraphics[height=5.25cm]{Capitulo5/Graficas5/loopstonha}](img751.gif)