5.3.3 Periodic Model
Figure:
The magnetization distribution at remanence calculated in
the periodic array of antidots for the external field
applied at 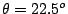 to the easy axis direction and
showing the occurrence of magnetic
inhomogeneities at the antidot surfaces. Every arrow gives the
average direction of a group of
to the easy axis direction and
showing the occurrence of magnetic
inhomogeneities at the antidot surfaces. Every arrow gives the
average direction of a group of 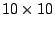 moments.
moments.
|
|
Figure:
Sequence of non-equilibrium magnetization configurations calculated in
the domain wall model for the external field
applied at  corresponding to the first jump of the
hysteresis loop.
corresponding to the first jump of the
hysteresis loop.
|
|
To get a deeper insight into the mechanisms involved in the angular
dependence of hysteresis we have performed micromagnetic simulations
considering two different models. In both of them the computational
region was discretized in a two-dimensional square mesh of 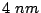 single layer units. In our first model, which will be referred as
``periodic model'', we
have considered an infinite array of antidots, corresponding to
periodic boundary conditions along X and Y directions and a
single layer units. In our first model, which will be referred as
``periodic model'', we
have considered an infinite array of antidots, corresponding to
periodic boundary conditions along X and Y directions and a  modeled
region including a circular antidot with
modeled
region including a circular antidot with 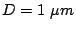 .
The remanent state was very similar to
the saturation in the easy axis direction except for the presence of
inhomogeneous
moment structures similar to closure domains at
the regions of the antidot surfaces (see Fig. 5.16). The thickness
of these regions, measured along the average moment
direction, was of the order of two times the exchange
length of Fe. In the antidot perimeter the magnetization is parallel to
the surface except in two small zones where it is parallel to the easy
axes.
The magnetization at remanence in the center between the antidots is
almost directed in the easy axis direction for any applied field angle
and the expected
.
The remanent state was very similar to
the saturation in the easy axis direction except for the presence of
inhomogeneous
moment structures similar to closure domains at
the regions of the antidot surfaces (see Fig. 5.16). The thickness
of these regions, measured along the average moment
direction, was of the order of two times the exchange
length of Fe. In the antidot perimeter the magnetization is parallel to
the surface except in two small zones where it is parallel to the easy
axes.
The magnetization at remanence in the center between the antidots is
almost directed in the easy axis direction for any applied field angle
and the expected  behavior is verified for the normalized
remanence
behavior is verified for the normalized
remanence 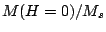 as a function of the applied field angle
as a function of the applied field angle 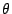 .
.
The angular dependence of the
demagnetization is governed by the occurrence of a
nucleation-propagation sequence starting from those inhomogeneous
magnetic moments structures present at the antidot surfaces and
resulting from the magnetostatic energy minimization. The process is
shown in Fig. 5.17. The results
obtained within this model show
the presence of two magnetization jumps (see Fig. 5.18 (a)) for almost all applied field
angles (the exceptions are the directions close to the h.a.) and
switching field values similar to those observed experimentally.
However, the calculated behavior of the angular dependence of the
first switching field (see Fig. 5.18(b))
is
qualitatively different from that experimentally observed.
Figure 5.18:
(a) Hysteresis loops and (b) angular dependence of the switching fields
in the antidots
arrays simulated in the periodic model in comparison to the
experimentally measured values.
|
|
|
|
2008-04-04
![\includegraphics[height=7.cm]{Capitulo5/Graficas5/KerrFigure4}](img753.gif)
![\includegraphics[width=0.8\textwidth]{Capitulo5/Graficas5/configurper}](img754.gif)