Figure:
Sequence of non-equilibrium magnetization configurations calculated in
the domain wall model for the external field
applied at 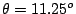 corresponding to the first jump
of the hysteresis loop.
corresponding to the first jump
of the hysteresis loop.
|
|
Our second model, which will be referred as ``domain wall model'',
consists of a 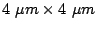 system
with a
centered array of
system
with a
centered array of 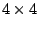 antidots of diameters
antidots of diameters
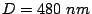 ,
separated by
,
separated by  . In order to implement a more
realistic approach to the experimental situation, we artificially
introduced a domain wall outside the antidots region allowing
to analyze the influence on the antidots magnetization reversal of
the lower field reversal of the perimetral region. To introduce the
domain wall, the anisotropy constant was set to be zero in two regions
of size
. In order to implement a more
realistic approach to the experimental situation, we artificially
introduced a domain wall outside the antidots region allowing
to analyze the influence on the antidots magnetization reversal of
the lower field reversal of the perimetral region. To introduce the
domain wall, the anisotropy constant was set to be zero in two regions
of size 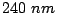 parallel
and next to two of the simulated square sides (like a half frame). This
domain wall exists already at the remanence and subsequent negative
field values. This is a realistic assumption since the reversal field
of the external region in experiment is several times inferior to that
of the antidot-induced demagnetization processes. The remanence
magnetization configuration in the interantidot region is similar to
the obtained in the periodic model and the
parallel
and next to two of the simulated square sides (like a half frame). This
domain wall exists already at the remanence and subsequent negative
field values. This is a realistic assumption since the reversal field
of the external region in experiment is several times inferior to that
of the antidot-induced demagnetization processes. The remanence
magnetization configuration in the interantidot region is similar to
the obtained in the periodic model and the
 dependence of the
normalized remanence is also obtained. As experimentally, we observe
two jumps except in the hard and easy axes configuration (see Fig. 5.20(a)). For a given field value the created
domain wall triggers an additional domain wall that reverses all the
sample as shown Fig. 5.19. As the
domain wall passes by the different antidots, the magnetization changes
to the intermediate easy axis direction and does not align in the field
direction. The external zone has completely reversed but the antidot
zone is aligned in the intermediate easy axis direction and that fact
creates a domain wall in the outer region pinned at the antidot
structure. After the first jump the magnetization rotates reversibly to
the field direction. The process corresponding to the second jump is
also an inhomogeneous process initiated in the outer line of antidots
nearest to the external domain wall.
dependence of the
normalized remanence is also obtained. As experimentally, we observe
two jumps except in the hard and easy axes configuration (see Fig. 5.20(a)). For a given field value the created
domain wall triggers an additional domain wall that reverses all the
sample as shown Fig. 5.19. As the
domain wall passes by the different antidots, the magnetization changes
to the intermediate easy axis direction and does not align in the field
direction. The external zone has completely reversed but the antidot
zone is aligned in the intermediate easy axis direction and that fact
creates a domain wall in the outer region pinned at the antidot
structure. After the first jump the magnetization rotates reversibly to
the field direction. The process corresponding to the second jump is
also an inhomogeneous process initiated in the outer line of antidots
nearest to the external domain wall.
Figure 5.20:
(a) Hysteresis loops and (b) angular dependence of the switching fields
in the antidots
arrays simulated in the domain wall model in comparison to the
experimentally measured values.
|
|
|
|
Alternatively, the nucleation of the external domain wall was also
implemented by assuming a triangular region, 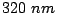 wide, with null anisotropy located at one
of the
system corners. Only one jump in the magnetization was obtained for all
the angles using that implementation.
Regarding the angle dependence of the field values for the jumps
appearing in the magnetization, the simulation with the ``half frame''
model and the experimental values are in very good agreement both in
quality and in magnitude (see Fig. 5.20 (b))
indicating that the reversal in the antidot regions involves a domain
wall created by the reversal of the external zone.
The occurrence of only one jump when the domain wall is created at the
corner is due to the fact that the event there is triggered for field
values larger than the ones necessary to observe the second jump.
In these simulations the nucleation in the antidot region, equivalent
to that of the periodic model (see Fig. 5.18), is also absent,
presumably because the simulation size in this case is different to the
simulated in Section 5.3.3.
wide, with null anisotropy located at one
of the
system corners. Only one jump in the magnetization was obtained for all
the angles using that implementation.
Regarding the angle dependence of the field values for the jumps
appearing in the magnetization, the simulation with the ``half frame''
model and the experimental values are in very good agreement both in
quality and in magnitude (see Fig. 5.20 (b))
indicating that the reversal in the antidot regions involves a domain
wall created by the reversal of the external zone.
The occurrence of only one jump when the domain wall is created at the
corner is due to the fact that the event there is triggered for field
values larger than the ones necessary to observe the second jump.
In these simulations the nucleation in the antidot region, equivalent
to that of the periodic model (see Fig. 5.18), is also absent,
presumably because the simulation size in this case is different to the
simulated in Section 5.3.3.
In the examined cases the antidot demagnetization process is not
determined by the antidot itself but by the defects and nucleation
sites in the non-lithographed area. The existing
possibilities for a nucleation-propagation-pinning sequence are
multiple and may be influenced by the presence of defects of
different types whose nature is determined by the deposition or
lithography techniques. This is a non desirable effect since we can not
control the presence of the defects and the aim of the antidots was to
externally control the coercivity of the film. On the other hand, we
have seen that even in this case, due to the presence of the antidots,
the coercivity of the film is enhanced.
2008-04-04
![\includegraphics[width=0.8\textwidth]{Capitulo5/Graficas5/configuraciones}](img759.gif)
![\includegraphics[width=\textwidth]{Capitulo5/Graficas5/wall3d}](img765.gif)
![]() wide, with null anisotropy located at one
of the
system corners. Only one jump in the magnetization was obtained for all
the angles using that implementation.
Regarding the angle dependence of the field values for the jumps
appearing in the magnetization, the simulation with the ``half frame''
model and the experimental values are in very good agreement both in
quality and in magnitude (see Fig. 5.20 (b))
indicating that the reversal in the antidot regions involves a domain
wall created by the reversal of the external zone.
The occurrence of only one jump when the domain wall is created at the
corner is due to the fact that the event there is triggered for field
values larger than the ones necessary to observe the second jump.
In these simulations the nucleation in the antidot region, equivalent
to that of the periodic model (see Fig. 5.18), is also absent,
presumably because the simulation size in this case is different to the
simulated in Section 5.3.3.
wide, with null anisotropy located at one
of the
system corners. Only one jump in the magnetization was obtained for all
the angles using that implementation.
Regarding the angle dependence of the field values for the jumps
appearing in the magnetization, the simulation with the ``half frame''
model and the experimental values are in very good agreement both in
quality and in magnitude (see Fig. 5.20 (b))
indicating that the reversal in the antidot regions involves a domain
wall created by the reversal of the external zone.
The occurrence of only one jump when the domain wall is created at the
corner is due to the fact that the event there is triggered for field
values larger than the ones necessary to observe the second jump.
In these simulations the nucleation in the antidot region, equivalent
to that of the periodic model (see Fig. 5.18), is also absent,
presumably because the simulation size in this case is different to the
simulated in Section 5.3.3.