Figure 5.6:
Measured coercivity of different samples plotted versus the inverse of
the interantidot distance (extracted from the Ph. D. thesis of J.M.
Torres [Torres 05]).
|
|
The coercivity of series of Fe antidot arrays was studied by J. M.
Torres [Torres 05]. The
arrays were produced by using X-ray lithography on a 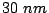 thick Fe(001)/GaAs film grown by Molecular
Beam Epitaxy in the group of Prof. J.A.C. Bland in the Cavendish
Laboratory (Cambridge). The lithographed region covered a
thick Fe(001)/GaAs film grown by Molecular
Beam Epitaxy in the group of Prof. J.A.C. Bland in the Cavendish
Laboratory (Cambridge). The lithographed region covered a
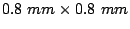 area out
of a
area out
of a 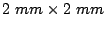 film. The samples prepared had
the following set of diameters and separation (D,
film. The samples prepared had
the following set of diameters and separation (D,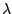 ): (
): (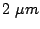 ,
, 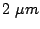 ), (
), ( ,
,  ), (
), (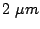 ,
, 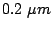 ) and (
) and ( ,
,
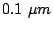 ). The
coercivity was
measured in the easy axis and hard axis configurations
using an alternating gradient field magnetometer (AGFM) in the
Instituto de Ciencia de Materiales de Aragón. The samples
presented two jump in the hysteresis loops in
both configurations: the first jump had a very similar value to that
of the samples before the lithography procedure. This jump corresponds
to the switching of the non-lithographed area. The second jump
corresponds to the
interantidot area. That later jump value can be several times higher
than the former. This fact can be assigned to the stabilizing role
of the antidots. Both processes can not be considered ``a priori''
independent, since the switching of the antidot region can be caused by
the external region. As expected, the obtained coercivities in easy
axis configuration are larger than the hard axis ones. Plotting the
value of this second jump as a
function of
). The
coercivity was
measured in the easy axis and hard axis configurations
using an alternating gradient field magnetometer (AGFM) in the
Instituto de Ciencia de Materiales de Aragón. The samples
presented two jump in the hysteresis loops in
both configurations: the first jump had a very similar value to that
of the samples before the lithography procedure. This jump corresponds
to the switching of the non-lithographed area. The second jump
corresponds to the
interantidot area. That later jump value can be several times higher
than the former. This fact can be assigned to the stabilizing role
of the antidots. Both processes can not be considered ``a priori''
independent, since the switching of the antidot region can be caused by
the external region. As expected, the obtained coercivities in easy
axis configuration are larger than the hard axis ones. Plotting the
value of this second jump as a
function of 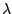 a hypothesis of the linear dependence with the inverse
of
a hypothesis of the linear dependence with the inverse
of 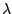 was
suggested (see Fig. 5.6) [Ruiz-Feal 02]. From that, the
coercivity was supposed to follow a simple scaling law with the inverse
of
was
suggested (see Fig. 5.6) [Ruiz-Feal 02]. From that, the
coercivity was supposed to follow a simple scaling law with the inverse
of 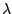 .
Generally speaking, the geometrical parameters
.
Generally speaking, the geometrical parameters 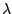 and
and  of every sample were different, and,
therefore, the coercivity can not be plotted as a
variation of a single parameter. Nevertheless, there is a increase of
the coercivity with the reduction of the distance
of every sample were different, and,
therefore, the coercivity can not be plotted as a
variation of a single parameter. Nevertheless, there is a increase of
the coercivity with the reduction of the distance 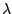 , but this dependence can be more complex
than the one shown in Fig. 5.6. More
ample series of sample are needed in order to verify the scaling
law. Series in which one of the parameters is kept constant are
specially interesting.
2008-04-04
, but this dependence can be more complex
than the one shown in Fig. 5.6. More
ample series of sample are needed in order to verify the scaling
law. Series in which one of the parameters is kept constant are
specially interesting.
2008-04-04
![\includegraphics[height=7.cm]{Capitulo5/Graficas5/leyescala}](img724.gif)