Figure:
Calculated coercive force dependence on the interantidot distance 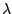 , for
, for 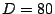 and
and 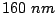 (easy, EA, and hard,
HA, axis data) from the calculations in the Ph. D. thesis of J.M.
Torres [Torres 05].
(easy, EA, and hard,
HA, axis data) from the calculations in the Ph. D. thesis of J.M.
Torres [Torres 05].
|
|
Trying to check the validity of the scaling law, in collaboration with
J.M. Torres [Torres Bruna 05]
we performed micromagnetic
simulations, varying the geometrical parameters. It is this kind of
problems where the utility of micromagnetic simulations is revealed,
allowing to study the magnetic behavior where the experimental data are
not available. Unfortunately, the sizes of the sample make impossible
to reach, within the available resources, the real dimensions of the
sample. A single periodicity cell was used but with periodic boundary
conditions. The results obtained from that simulation showed two
different types of behavior, each corresponding to a different
concentration regime. For small values 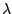 , concentrated regime, there is a strong
dependence on
, concentrated regime, there is a strong
dependence on 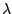 of the coercivity. The corresponding magnetic configuration is shown in
Fig. 5.8(c), where clearly a domain
structure is formed. For large values of
of the coercivity. The corresponding magnetic configuration is shown in
Fig. 5.8(c), where clearly a domain
structure is formed. For large values of 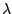 , diluted regime, the coercivity becomes
independent of
, diluted regime, the coercivity becomes
independent of 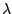 .
In this case the flux closure structures occupy a small portion of the
film as in Fig. 5.8(a). A minimum of
coercivity is obtained in the crossover between the two types of
behavior. This corresponds to the case where the magnetic structures of
closest antidots join each other (see Fig. 5.8(b)).
In
the simulations a similar behavior to the experimental one is observed
if only small
.
In this case the flux closure structures occupy a small portion of the
film as in Fig. 5.8(a). A minimum of
coercivity is obtained in the crossover between the two types of
behavior. This corresponds to the case where the magnetic structures of
closest antidots join each other (see Fig. 5.8(b)).
In
the simulations a similar behavior to the experimental one is observed
if only small 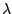 region is taken into account, but for simulated sizes much smaller than
in real samples.
region is taken into account, but for simulated sizes much smaller than
in real samples.
Figure:
Magnetic moment configuration slightly before the array magnetization
reversal for 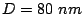 and the following parameter values: a)
and the following parameter values: a) 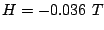 and
and 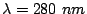 , b)
, b) 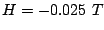 and
and  , and c)
, and c) 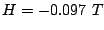 and
and 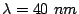 from the
calculations in the Ph. D. thesis of J.M. Torres [Torres 05].
from the
calculations in the Ph. D. thesis of J.M. Torres [Torres 05].
|
|
|
|
In real samples the demagnetization process can be determined by the
nucleation of a domain wall in the exterior region, specially in the
diluted regimen. In the simulations of periodic structure this domain
wall was absent, but can be included using open boundary conditions in
one of the in-plane directions. The influence of the external zone was
analyzed using the same range sizes [Gonzalez 05]. The presence
of the external domain wall reduced the coercivity but the qualitative
behavior was preserved. The pinning of the domain wall by the outer
antidots was also observed.
2008-04-04
![\includegraphics[height=7.cm]{Capitulo5/Graficas5/simuljm}](img729.gif)
![\includegraphics[width=\textwidth]{Capitulo5/Graficas5/configurjm}](img730.gif)