The magnetostatic self energy is the interaction of a distribution of a magnetization vector with the magnetic field created by this distribution itself. This energy term is normally written in the following way:
 |
(118) |
where the integration is over the volume of the ferromagnetic system, taken as a continuum. Due to its long range character, the magnetostatic interaction generally depends on the shape of the system, and it is responsible for the existence of magnetic domains. Usually this contribution leads to the commonly called shape anisotropy, and becomes important in thin films where it often produces in-plane alignment of moments. The proper calculation of the magnetostatic energy belongs to the area of micromagnetism and is computationally costly.
As a first approximation of the magnetostatic anisotropy energy, we used a simplified version of the demagnetization factor approach valid for thin films with homogeneous magnetization [180]. Then the density of energy per volume could be written as an additional anisotropy term [181,182].
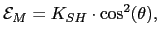 |
(119) |
where
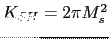 in c.g.s. unit system. The magnetization makes an angle (
in c.g.s. unit system. The magnetization makes an angle (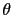 ) to the plane normal. The magnetostatic anisotropy energy is thus minimized for an angle of
) to the plane normal. The magnetostatic anisotropy energy is thus minimized for an angle of
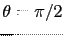 , this implies all the moments lying in the plane of the thin film.
, this implies all the moments lying in the plane of the thin film.
The saturation magnetization  is related at
is related at 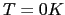 to the atomic magnetic moment
to the atomic magnetic moment 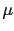 through:
through:
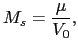 |
(120) |
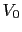 represents the atomic volume. In the case of an fcc lattice the atomic volume is related with the lattice parameter a as
represents the atomic volume. In the case of an fcc lattice the atomic volume is related with the lattice parameter a as
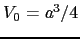 (for Co
(for Co
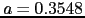 nm). As we can see in section 6.3.3, the orbital magnetic moment in Co system is practically zero, because of that the atomic magnetic moment in this case is taken as:
nm). As we can see in section 6.3.3, the orbital magnetic moment in Co system is practically zero, because of that the atomic magnetic moment in this case is taken as:
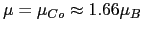 . Then we obtain that
. Then we obtain that
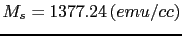 at
at 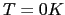 .
.
The expression (6.42) represents the magnetostatic energy for a thin films with a homogeneous magnetization. In our case we have a layered system with a total magnetostatic energy in the form similar to that described in Ref. [115]:
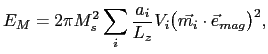 |
(121) |
here the sum is up to the total number of spin N,  is the saturation magnetization,
is the saturation magnetization, 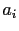 is the width of the atomic layer i,
is the width of the atomic layer i,  is the thickness of the thin film,
is the thickness of the thin film, 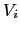 is the atomic volume of the spin i,
is the atomic volume of the spin i,
 is the unit vector in the direction of the magnetization at site i,
is the unit vector in the direction of the magnetization at site i,
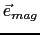 is the magnetostatic anisotropy axis, in the case of thin films,
is the magnetostatic anisotropy axis, in the case of thin films,
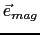 is perpendicular to the plane of the surface, which favors the orientation of the magnetization in plane.
is perpendicular to the plane of the surface, which favors the orientation of the magnetization in plane.
In our case, the direction perpendicular to the surface of the thin films is parallel to Z axis. The expression above is reduced to the following one:
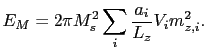 |
(122) |
In the approximation described above we implicity supposed that the
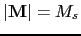 , this means that it is an athermal approximation. Nevertheless in our work we want to analyze the magnetic behavior of our system at
, this means that it is an athermal approximation. Nevertheless in our work we want to analyze the magnetic behavior of our system at 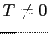 , therefore we have to introduce the temperature effects on the magnetostatic energy.
In this case the value of
, therefore we have to introduce the temperature effects on the magnetostatic energy.
In this case the value of  should be substituted by
should be substituted by
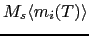 . In this way the magnetostatic energy can be written as:
. In this way the magnetostatic energy can be written as:
 |
(123) |
here
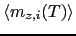 is the average z component of the magnetization at the atomic plane to which the spin i belongs for a temperature T.
Rocio Yanes
is the average z component of the magnetization at the atomic plane to which the spin i belongs for a temperature T.
Rocio Yanes

![]() is related at
is related at ![]() to the atomic magnetic moment
to the atomic magnetic moment ![]() through:
through:
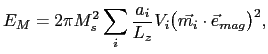
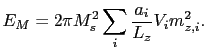
![]() , this means that it is an athermal approximation. Nevertheless in our work we want to analyze the magnetic behavior of our system at
, this means that it is an athermal approximation. Nevertheless in our work we want to analyze the magnetic behavior of our system at ![]() , therefore we have to introduce the temperature effects on the magnetostatic energy.
In this case the value of
, therefore we have to introduce the temperature effects on the magnetostatic energy.
In this case the value of ![]() should be substituted by
should be substituted by
![]() . In this way the magnetostatic energy can be written as:
. In this way the magnetostatic energy can be written as:
