At this point, we linked the physical magnitudes extracted from the "ab-initio" simulations where the electronic structure has been explicitly taken into account to an atomistic semiclassical model, in which every magnetic parameter: magnetic moment, anisotropy constant, exchange coupling etc., has its value at the atom site. This can be described as follows:
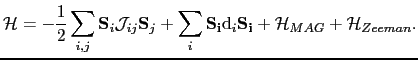 |
(117) |
Here the exchange interaction and on-site anisotropy (
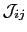 and
and
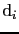 ) are expressed in a general form, where they are
) are expressed in a general form, where they are 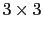 matrices.
The Hamiltonian of the system has the form of a generalized Heisenberg Hamiltonian, where the first term corresponds to various exchange contributions, and in the double sum of the exchange interactions terms the indices i y j range from 1 to N excluding the case
matrices.
The Hamiltonian of the system has the form of a generalized Heisenberg Hamiltonian, where the first term corresponds to various exchange contributions, and in the double sum of the exchange interactions terms the indices i y j range from 1 to N excluding the case 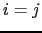 , where N represents the total number of the spins in the system. The second term is the on-site anisotropy energy,
, where N represents the total number of the spins in the system. The second term is the on-site anisotropy energy,
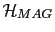 is the magnetostatic energy term, and the last term
is the magnetostatic energy term, and the last term
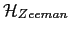 corresponds to the Zeeman energy.
corresponds to the Zeeman energy.
In this section we focus our efforts on the study of the magnetic behavior of a thin film of
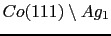 with fcc lattice structure. From the first principle calculations we have extracted the magnetic parameters that are used to perform temperature-dependent simulations. We also make some assumptions:
with fcc lattice structure. From the first principle calculations we have extracted the magnetic parameters that are used to perform temperature-dependent simulations. We also make some assumptions:
- We assume that the Ag magnetic moments, exchange and anisotropy are negligible due to their small values. Then the Hamiltonian takes into account Co moments only.
- In our simulations there are no external applied magnetic field, therefore the Zeeman contribution to the total energy is zero.
- Although the "ab-initio" results (see section 6.3.3) showed some increment of the spin and orbital Co moments at the interface of the
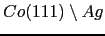 system, in the first approximation to the problem we assume that the cobalt's moments are the same as those in the bulk system. As is shown in Table (6.2) these modifications are in practice negligible.
system, in the first approximation to the problem we assume that the cobalt's moments are the same as those in the bulk system. As is shown in Table (6.2) these modifications are in practice negligible.
Subsections
Rocio Yanes
![]() with fcc lattice structure. From the first principle calculations we have extracted the magnetic parameters that are used to perform temperature-dependent simulations. We also make some assumptions:
with fcc lattice structure. From the first principle calculations we have extracted the magnetic parameters that are used to perform temperature-dependent simulations. We also make some assumptions: