Next: 4 Temperature-dependent macroscopic properties Up: 5 Magneto-crystalline anisotropy energy Previous: 4 Magneto-crystalline anisotropy energy Contents
Here we present a detailed study of the MCA energy for a particular system of
![]() . The first step is to obtain the angular dependence of the energy. In Fig. 6.13, we show the band energy of the system
. The first step is to obtain the angular dependence of the energy. In Fig. 6.13, we show the band energy of the system
![]() as a function of the angle (
as a function of the angle (![]() ) from the Z axis (axis perpendicular to the surface of the thin film). The value obtained from SKKR calculation has been compared with the analytical expression of the angular dependence of the uniaxial anisotropy energy, showing that both adjust perfectly.
) from the Z axis (axis perpendicular to the surface of the thin film). The value obtained from SKKR calculation has been compared with the analytical expression of the angular dependence of the uniaxial anisotropy energy, showing that both adjust perfectly.
![\includegraphics[totalheight=0.35\textheight]{co5ag1_111_EbT.eps}](img939.gif)
|
 |
(115) |
As we presented in previous section (6.3.5), the effective anisotropy constant extracted from the "ab-initio" calculations is related to the difference of the band energy between the magnetic moments configuration oriented at different directions,
![]() and
and
![]() . The problem appears when we try to figure out which are different contributions to this effective anisotropy. In the first place, we have an on-site contribution (
. The problem appears when we try to figure out which are different contributions to this effective anisotropy. In the first place, we have an on-site contribution (![]() ). As we mentioned in section (6.3.4) the anisotropic part of the exchange tensor interaction also contributes to the anisotropy, with a two-site anisotropy contribution, in a such way that:
). As we mentioned in section (6.3.4) the anisotropic part of the exchange tensor interaction also contributes to the anisotropy, with a two-site anisotropy contribution, in a such way that:
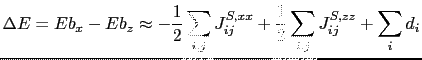 |
(116) |
![[*]](footnote.gif) we can get the layer-resolved on-site anisotropy constant
we can get the layer-resolved on-site anisotropy constant
Rocio Yanes