5 Magneto-crystalline anisotropy energy

The magneto-crystalline anisotropy (MCA) energy has its origin in the spin-orbit coupling under the ordering imposed by the crystalline lattice of the material. In the most general case, the magnetocrystalline anisotropy matrix $d_{i}$ can be written as a function of its eigenvectors (corresponding to the easy axes) $u_{i}^{\alpha}$ and eigenvalues $d_{i}^{\alpha\alpha}$:

$$\mathbf{\mathrm{d}_{i}}=\sum_{\alpha=1,2,3}d_{i}^{\alpha\alpha}u_{i}^{\alpha}(u_{i}^{\alpha})^{T}$$ (109)

In this general case we have a triaxial anisotropy. This sort of anisotropy could be present in a system with a reduced symmetry such as surfaces, edges, etc. The contribution due to the on-site anisotropy to the total energy has the following form:

$$\mathcal{H}_{ani}= \sum_{i}\mathrm{d(\mathbf{S_{i}})}= \sum_{i}\m... ...\sum_{\alpha=1,2,3}d_{i}^{\alpha\alpha}(\mathbf{S_{i}}\cdot u_{i}^{\alpha})^{2}$$ (110)

Epitaxially grown systems present usually uniaxial anisotropy. If we suppose that in this case the easy axis is parallel to the Z axis, then the on-site anisotropy has the form:

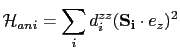$$\mathcal{H}_{ani}= \sum_{i}d_{i}^{zz}(\mathbf{S_{i}}\cdot e_{z})^{2}$$ (111)

We have only described the on-site magneto-crystalline anisotropy. However, there could exist other contributions to the magnetic anisotropy of the system, as e.g. the two-site magnetic anisotropy, mentioned already above and discussed later in this chapter.