Next: 2 Magneto-crystalline anisotropy energy Up: 5 Magneto-crystalline anisotropy energy Previous: 5 Magneto-crystalline anisotropy energy Contents
The evaluation of the total magneto-crystalline anisotropy energy with the Budapest-Vienna SKKR code is based on the so-called "force theorem" [167,86,142]. Within this approximation, for each system two calculations were performed, using the previously determined self-consistent potentials.
Namely the first calculation with the magnetic field perpendicular to the surface ![]() and the second with the magnetic filed pointing along X axis, which is one of the crystalline axis contained in the plane of the surface
and the second with the magnetic filed pointing along X axis, which is one of the crystalline axis contained in the plane of the surface ![]() .
.
Typically the MCA energy in transition metals is small, of the order of a few tens of ![]() , and this is the real difficulty in performing such calculations with a good accuracy of the results. For this reason it is necessary to perform a previous study of the convergence of the value of
, and this is the real difficulty in performing such calculations with a good accuracy of the results. For this reason it is necessary to perform a previous study of the convergence of the value of
![]() with respect to the number of k (wave number) points for energies close to the Fermi energy
with respect to the number of k (wave number) points for energies close to the Fermi energy ![]() . Such stability study has been done for all the systems which we have analyzed.
Once we have obtained the value of the MCA energy, we can extract the corresponding value of the effective anisotropy constant
. Such stability study has been done for all the systems which we have analyzed.
Once we have obtained the value of the MCA energy, we can extract the corresponding value of the effective anisotropy constant ![]() . The anisotropy constant is an energy density and can be described as:
. The anisotropy constant is an energy density and can be described as:
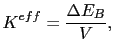 |
(113) |
In the next sections we will discuss the MCA behavior with different surface's orientations and cappings. Later, we will obtain the layer resolved MCA for different systems. The next point in our study will be to understand how the MCA is affected with the relaxation of the lattice. To conclude this section we will analyze different contributions to the MCA energy for a particular system
![]() .
.