4 Antisymmetric anisotropic exchange tensor

The third term in equation (6.25) represents the Dzyaloshinsky-Moriya (DM) interaction [175,176]. The DM contribution to the Hamiltonian of the system has the following form:

$$\mathcal{H}^{ex}_{DM}=- \frac{1}{2}\sum_{i,j}\mathbf{D}_{ij}\bigl(\mathbf{S_{i}}\times\mathbf{S_{j}}\bigr)\: ,$$ (108)

where the $\mathbf{D}_{ij}$ is Dzyaloshinsky-Moriya vector and is defined as:

$$D_{ij}^{x} = \frac{1}{2}(J_{ij}^{yz}-J_{ij}^{zy})$$

$$D_{ij}^{y} = \frac{1}{2}(J_{ij}^{xz}-J_{ij}^{zx})$$

$$D_{ij}^{z} = \frac{1}{2}(J_{ij}^{xy}-J_{ij}^{yx})$$

$\mathbf{D}_{ij}$ is zero if sites i and j experience an inversion symmetry. Therefore, this contribution is practically zero in bulk system. Nevertheless the DM term can be enhanced near the magnetic surface due to the reduction of the symmetry. It also tends to lower the energy of the system upon inducing a non-collinear spin-structure [177,178]. To clarify the DM contribution in different systems, we present in Tab. 6.4 the value of the module of DM vector for the first nearest neighbors, in Co (fcc, bulk) and for the surface layer or the interface in Co(100), $Co(100)\setminus Ag_{1}$ and $Co(111)\setminus Ag_{1}$.

Table 6.4: Calculated module of the DM vectors $\mid \mathbf {D_{ij}}\mid$ (all in meV) for the first nearest neighbors in Co (fcc, bulk) surface of Co fcc (100), $Co(100)\setminus Ag_{1}$ and $Co(111)\setminus Ag_{1}$.

System	Co(bulk)	Co(100)	$\mathbf{Co(100)\setminus Ag_{1}}$	$\mathbf{Co(111)\setminus Ag_{1}}$
$\mid \mathbf {D_{ij}}\mid$	0.0	0.475	0.58	0.408

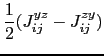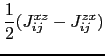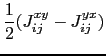As we have expected in the case of a Co bulk system the DM is zero. From the results for $\mid \mathbf {D_{ij}}\mid$ presented in Tab. 6.4 we can conclude that the Dzyaloshinsky-Moriya interaction is modified, if the surface of Co(100) is capped by an Ag layer. In this case the module of a DM vector between nearest neighbors is increased, but it decays more rapidly than in the case of free Co(100) surface, and the direction of the DM vector at second nearest neighbors is changed (see Fig. 6.10).

The increment of $\mid \mathbf {D_{ij}}\mid$ in the case of $Co(100)\setminus Ag_{1}$ with respect to the corresponding value in Co(100) surface could be due to the pure effect of the Ag capping and also due to the existence of a relaxation in the lattice. We can find cases where the relaxation affects the value of the DM interaction, for example we can mention the case of $Fe_{2}\setminus W(110)$, in this case as the relaxation of the lattice is decreased from $26\%$ to $10\%$, the magnitude of the main DM interaction is reduced by about three times [178].

Figure 6.10: Sketch of the DM vectors for (a) Co(100) surface, (b) $Co(100)\setminus Ag_{1}$ interface and (c) $Co(111)\setminus Ag_{1}$ interface. For the cases of $Co\setminus Ag$ systems the lattice relaxation is of $10\%$, the arrows indicate the direction of the DM vectors, and the values are normalized to the maximum of DM module ( $\mid \mathbf {D_{ij}}\mid$ for each system.)

The Dzyaloshinsky-Moriya contribution to the total exchange matrix is much smaller, approximately two orders of magnitude lower, than the isotropic exchange one. However it is comparable to that of the on-site anisotropy. Therefore we have to study in each particular case how important is this contribution in the effective magnetic anisotropy energy of the system.

The calculated DM vectors for three systems are displayed in Fig. 6.10 (a) Co(100) surface, (b) $Co(100)\setminus Ag_{1}$ interface and (c) $Co(111)\setminus Ag_{1}$. For the cases of $Co\setminus Ag$ systems the lattice relaxation is $r=10\%$, the arrows indicate the directions of the DM vectors, and the values are normalized to the maximum value of DM vectors module $\mid \mathbf {D_{ij}}\mid$ for each system (shows in Tab. 6.4). In the cases (a-b) which correspond to the (100) surface/ interface, the DM vectors lie in the surface/interface plane, which implies that an orientation of the Co spins perpendicular to the surface/interface is favored. While in the case (c) (111) interface, the DM vectors are oriented practically perpendicular to the interface, which favors an in-plane orientation of the Co spins at the interface. As we have mentioned above, the DM vectors in Fig. 6.10 are normalized, this allows us to note that DM interaction, in the same way as values of $J_{ij}$, diminishes very rapidly with the distance between the spins i and j.