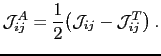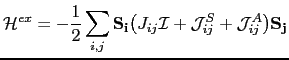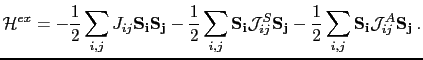There are different methods in the literature to map the first principle calculations to the exchange coupling parameters entering in a Heisenberg-like spin Hamiltonian. We have used in this chapter the magnetic "force theorem" [167,86,168]. It states that for the frozen ground state potential and small perturbations in the electron and magnetization densities (
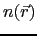 ,
,
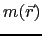 ), the variation of the total energy of the system can be approximated by the difference of the occupied single-particle state energies (
), the variation of the total energy of the system can be approximated by the difference of the occupied single-particle state energies (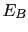 , called band energy).
Within the adiabatic approach the fast motion of the itinerant electrons is decoupled from the slow motion of the spins. This means that the electronic system is assumed to be at any instant in its ground state with respect to the orientation
, called band energy).
Within the adiabatic approach the fast motion of the itinerant electrons is decoupled from the slow motion of the spins. This means that the electronic system is assumed to be at any instant in its ground state with respect to the orientation
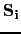 . This approximation is valid if the time scale of the precession of the magnetic moment is larger compared to that of the motion of electrons. It has been shown that in terms of the rigid-spin approximation the adiabatic dynamics of the local spin moments is described by the Landau-Lifshitz equation [169].
. This approximation is valid if the time scale of the precession of the magnetic moment is larger compared to that of the motion of electrons. It has been shown that in terms of the rigid-spin approximation the adiabatic dynamics of the local spin moments is described by the Landau-Lifshitz equation [169].
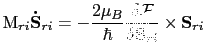 |
(94) |
where
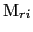 is the magnitude of the spin-moment of the spin i of the atomic layer r,
is the magnitude of the spin-moment of the spin i of the atomic layer r,
 is a unit vector pointing along the spin-quantization axis in the cell at site i of layer r,
is a unit vector pointing along the spin-quantization axis in the cell at site i of layer r,
 is the free-energy of the system and
is the free-energy of the system and  is the reduced Planck constant.
is the reduced Planck constant.
We will rewrite Eq. (6.17) into spherical coordinates (
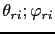 ), with polar and azimuthal angles, respectively, measured from the spin-quantization axis. Selecting the corresponding reference system and adopting the harmonic approximation, we can expand the Hamiltonian up to the second order of the free-energy
), with polar and azimuthal angles, respectively, measured from the spin-quantization axis. Selecting the corresponding reference system and adopting the harmonic approximation, we can expand the Hamiltonian up to the second order of the free-energy
 in angular variables
in angular variables![[*]](footnote.gif) . After that we can relate such Hamiltonian with a generalized Heisenberg Hamiltonian and determine the exchange matrix.
. After that we can relate such Hamiltonian with a generalized Heisenberg Hamiltonian and determine the exchange matrix.
The exchange matrix can be determined in ferromagnetic states by calculating the derivatives of the free energy, with respect to three orthogonal directions of the magnetization: X, Y and Z, see Ref. [142]. Then we get the following results for the magnetization parallel to the X direction:
For the magnetization parallel to the Y direction:
For the magnetization parallel to the Z direction:
Here i and j are different spin sites. In the way described above we have calculated the exchange tensor
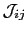 within the SKKR method using a full-relativistic description.
within the SKKR method using a full-relativistic description.
The exchange tensor
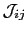 is a matrix
is a matrix
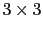 , its elements can be noted by
, its elements can be noted by
 where
where
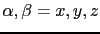 . It
. It
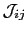 can be decomposed into three terms as in Ref. [142]:
can be decomposed into three terms as in Ref. [142]:
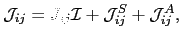 |
(95) |
where
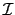 is the unit matrix and
is the unit matrix and 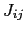 is the isotropic part of the exchange tensor:
is the isotropic part of the exchange tensor:
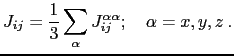 |
(96) |
This term is the parameter normally used as a classical exchange constant.
The second term
 is the traceless symmetric anisotropic exchange tensor and it is defined by
is the traceless symmetric anisotropic exchange tensor and it is defined by
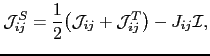 |
(97) |
where
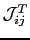 is the transpose of the exchange tensor.
is the transpose of the exchange tensor.
The third term
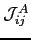 is the antisymmetric exchange matrix and it is given by
is the antisymmetric exchange matrix and it is given by
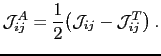 |
(98) |
Then we can rewrite the exchange part of the Hamiltonian (6.1) as a function of the isotropic, symmetric anisotropic and antisymmetric exchange as follows:
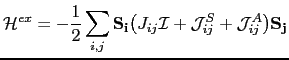 |
(99) |
This equation could be simplified in the following form:
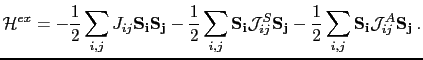 |
(100) |
The corresponding inter-site antisymmetric exchange interaction can be cast in the form, known as the Dzyaloshinsky-Moriya interaction.
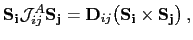 |
(101) |
where
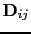 is the Dzyaloshinsky-Moriya vector.
is the Dzyaloshinsky-Moriya vector.
Finally,
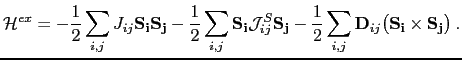 |
(102) |
Rocio Yanes
![]() ,
,
![]() ), the variation of the total energy of the system can be approximated by the difference of the occupied single-particle state energies (
), the variation of the total energy of the system can be approximated by the difference of the occupied single-particle state energies (![]() , called band energy).
Within the adiabatic approach the fast motion of the itinerant electrons is decoupled from the slow motion of the spins. This means that the electronic system is assumed to be at any instant in its ground state with respect to the orientation
, called band energy).
Within the adiabatic approach the fast motion of the itinerant electrons is decoupled from the slow motion of the spins. This means that the electronic system is assumed to be at any instant in its ground state with respect to the orientation
![]() . This approximation is valid if the time scale of the precession of the magnetic moment is larger compared to that of the motion of electrons. It has been shown that in terms of the rigid-spin approximation the adiabatic dynamics of the local spin moments is described by the Landau-Lifshitz equation [169].
. This approximation is valid if the time scale of the precession of the magnetic moment is larger compared to that of the motion of electrons. It has been shown that in terms of the rigid-spin approximation the adiabatic dynamics of the local spin moments is described by the Landau-Lifshitz equation [169].
![]() ), with polar and azimuthal angles, respectively, measured from the spin-quantization axis. Selecting the corresponding reference system and adopting the harmonic approximation, we can expand the Hamiltonian up to the second order of the free-energy
), with polar and azimuthal angles, respectively, measured from the spin-quantization axis. Selecting the corresponding reference system and adopting the harmonic approximation, we can expand the Hamiltonian up to the second order of the free-energy
![]() in angular variables
in angular variables![[*]](footnote.gif) . After that we can relate such Hamiltonian with a generalized Heisenberg Hamiltonian and determine the exchange matrix.
. After that we can relate such Hamiltonian with a generalized Heisenberg Hamiltonian and determine the exchange matrix.

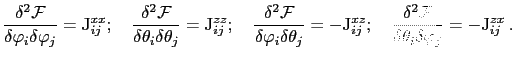
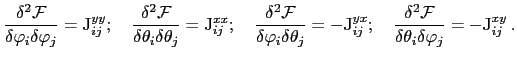
![]() is a matrix
is a matrix
![]() , its elements can be noted by
, its elements can be noted by
![]() where
where
![]() . It
. It
![]() can be decomposed into three terms as in Ref. [142]:
can be decomposed into three terms as in Ref. [142]:
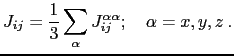
![]() is the traceless symmetric anisotropic exchange tensor and it is defined by
is the traceless symmetric anisotropic exchange tensor and it is defined by
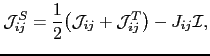
![]() is the antisymmetric exchange matrix and it is given by
is the antisymmetric exchange matrix and it is given by