Next: 3 Symmetric anisotropic exchange Up: 4 Exchange interactions Previous: 1 Evaluation of the Contents
![\includegraphics[totalheight=0.27\textheight]{Co_bulk_Joj_Dist.eps}](img869.gif)
![\includegraphics[totalheight=0.27\textheight]{Co_100_Joj_Dist.eps}](img870.gif)
|
The calculated values of the isotropic exchange interactions are shown as a function of the distance between Co atoms in a bulk Co fcc system and a semi-infinite Co fcc with (100) surface . In both cases we observe that the first nearest-neighbor exchange pair interactions have a ferromagnetic character, also we can see the oscillating behavior of the parameter ![]() with the distance.
The order of magnitude of the isotropic exchange interaction is in agreement with those presented in Refs. [170,171] for the cases of thin films of Co on Cu(001) and for Co bulk [172,40].
with the distance.
The order of magnitude of the isotropic exchange interaction is in agreement with those presented in Refs. [170,171] for the cases of thin films of Co on Cu(001) and for Co bulk [172,40].
We have to note the increment of the exchange pair interaction when the spins are close to the surface. This effects is clearly observed in the right pannel of Fig. 6.7. If we analyze in detail the graphic, we see that there is a decrease in the value of ![]() with the distance from the surface. Similar behaviour also occurs in
with the distance from the surface. Similar behaviour also occurs in
![]() system. Clearly, the isotropic exchange interaction values for nearest neighbors (NNs) depend on the position of the spin i, specifically on the atomic layer to which it belongs. The values of the isotropic exchange between NNs are also different if these NNs spins are coplanar or if they belong to different atomic layers.
system. Clearly, the isotropic exchange interaction values for nearest neighbors (NNs) depend on the position of the spin i, specifically on the atomic layer to which it belongs. The values of the isotropic exchange between NNs are also different if these NNs spins are coplanar or if they belong to different atomic layers.
With the aim to represent the behavior of the isotropic exchange interaction, we define two parameters ![]() and
and ![]() .
. ![]() is the isotropic exchange interaction between the spin i at layer p, and the spin j at layer q, and
is the isotropic exchange interaction between the spin i at layer p, and the spin j at layer q, and ![]() is the distance from the surface of the atomic layer of spin i. Here
is the distance from the surface of the atomic layer of spin i. Here
![]() , where
, where ![]() represents the label of the atomic surface (interface) layer, and
represents the label of the atomic surface (interface) layer, and ![]() is the plane index of the spin i. We have to note that when
is the plane index of the spin i. We have to note that when
![]() the spin i belongs to the surface or the interface, depending of the studied case.
the spin i belongs to the surface or the interface, depending of the studied case.
Then we can analyze the behavior of ![]() with the proximity of the surface.
with the proximity of the surface.
![\includegraphics[totalheight=0.27\textheight]{Jijpp_layer.eps}](img875.gif)
![\includegraphics[totalheight=0.27\textheight]{Jijpq_layer.eps}](img876.gif)
|
In Fig. 6.8 we plotted the calculated isotropic exchange interaction strength between the nearest neighbors in the same layer ![]() (left graph) and in different layers
(left graph) and in different layers ![]() (right graph) (in meV) as a function of
(right graph) (in meV) as a function of ![]() . The results are presented for Co(100) surface,
. The results are presented for Co(100) surface,
![]() and
and
![]() .
In both cases, for NN in the same or in different atomic layer, the isotropic exchange parameter increases in the proximity of the surface.
.
In both cases, for NN in the same or in different atomic layer, the isotropic exchange parameter increases in the proximity of the surface.
Despite the fact that an increase in ![]() on the surface described above exists, it is possible that the total exchange interaction will be smaller at the surface due to the loss of neighbors in that layer. With this aim we introduce an effective exchange interaction parameter,
on the surface described above exists, it is possible that the total exchange interaction will be smaller at the surface due to the loss of neighbors in that layer. With this aim we introduce an effective exchange interaction parameter,
![]() , defined as:
, defined as:
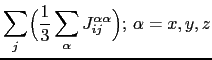 |
(103) |
In the left side of Fig. 6.9 we present this effective exchange interaction parameter as a function of the distance from the surface (interface) atomic layer (![]() ), in the various systems: Co (bulk), Co(100) surface,
), in the various systems: Co (bulk), Co(100) surface,
![]() and
and
![]() . Fig 6.9 shows that the
. Fig 6.9 shows that the
![]() parameter has practically the bulk value (black line) in the central atomic layers, but at surfaces its value decreases. This comes from the fact that at the surface or interface the number of the neighbors is drastically reduced. However the exchange interaction decays rapidly with the distance between neighbors, thus the surface effects are practically negligible at two atomic layers from the surface.
parameter has practically the bulk value (black line) in the central atomic layers, but at surfaces its value decreases. This comes from the fact that at the surface or interface the number of the neighbors is drastically reduced. However the exchange interaction decays rapidly with the distance between neighbors, thus the surface effects are practically negligible at two atomic layers from the surface.
![\includegraphics[totalheight=0.27\textheight]{Joz_layer.eps}](img879.gif)
![\includegraphics[totalheight=0.27\textheight]{Tc_layer.eps}](img880.gif)
|
The effective layer-resolved Curie temperature can be calculated from the value of the "effective" exchange interaction parameter using the mean-field expression:
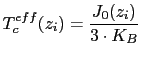 |
(104) |
Rocio Yanes