Next: 1 The studied system Up: 6 Multiscale modeling of Previous: 4 Screened Korringa-Kohn-Rostoker Green's Contents
The "ab-initio" calculations presented in this thesis are based on the fully relativistic Screened Korringa-Kohn-Rostoker (SKKR) Green's function method [86]. Within this method the spin-polarization and the relativistic effects are treated on equal theoretical footing by solving the Kohn-Sham-Dirac equation. We used the local spin-density approximation (LSDA) for the exchange-correlation term and the effective potential and field were treated within the atomic sphere approximation (ASA), with an angular momentun cutoff of ![]() .
.
In ASA the effective potential is of a muffin-tin type, surrounding each atom there is a sphere of radius ![]() outside of which the potential has a value equal to a constant, and within the sphere the potential is assumed to be spherically symmetric leaving only a radial dependence of the potential. Within ASA , the effective potential
outside of which the potential has a value equal to a constant, and within the sphere the potential is assumed to be spherically symmetric leaving only a radial dependence of the potential. Within ASA , the effective potential ![]() , at one atomic site can be written as:
, at one atomic site can be written as:
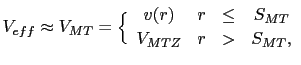 |
(93) |
Henceforth we will apply a spin-polarized relativistic version of the screened Korringa-Kohn-Rostoker Green's function method to calculate the magnetic properties: spin and orbital moments, exchange constants, and magnetocrystalline anisotropy energy. Once reached this point, we would like to point out some issues, which will be important throughout this chapter:
The theoretical and computational details of the SKKR method used in our calculations can be found in the Weinberger book [155].
First we will discuss the results of a self-consistent calculation of the work function, the spin and orbital moments in the ![]() layered system, after that we will analyze the results for the exchange interaction and the magneto-crystalline anisotropy (MCA) energy, obtained using the "magnetic force theorem". Finally we will study the magnetic behavior of a particular system
layered system, after that we will analyze the results for the exchange interaction and the magneto-crystalline anisotropy (MCA) energy, obtained using the "magnetic force theorem". Finally we will study the magnetic behavior of a particular system
![]() with the temperature.
with the temperature.