Next: 2 Contribution to total Up: A. Appendix A Previous: A. Appendix A Contents
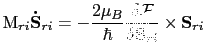 |
(125) |
where
![]() is a unit vector pointing along the spin-quantization axis in the atomic cell at the site i of the layer r,
is a unit vector pointing along the spin-quantization axis in the atomic cell at the site i of the layer r,
![]() is the magnitude of the spin moment and
is the magnitude of the spin moment and
![]() is the free energy of the system. If we are working in spherical coordinates then we can write
is the free energy of the system. If we are working in spherical coordinates then we can write
![]() as a function of the polar and azimuthal angles
as a function of the polar and azimuthal angles
![]() and
and
![]() respectively.
respectively.
| (126) |
If we choose the polar axis of the reference system (Z) perpendicular to the magnetization in the ferromagnetic state, the system of equations (A.3 and A.4) can be linearized
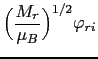 |
(131) | ||
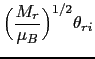 |
(132) |
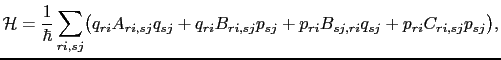 |
(133) |
with
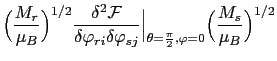 |
(134) | ||
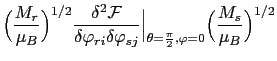 |
(135) | ||
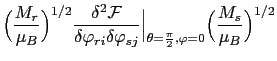 |
(136) |
Rocio Yanes