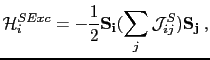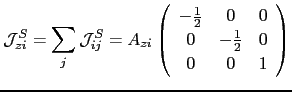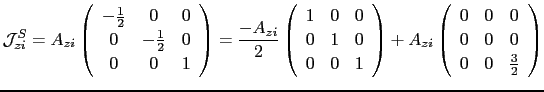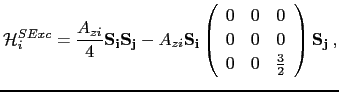2 Contribution to total uniaxial anisotropy due to "two-site" anisotropy
In chapter 6 we have shown that the contribution of the symmetric part of the exchange matrix interaction to the Hamiltonian (
 ) can be written as follows:
) can be written as follows:
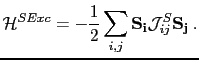 |
(137) |
The double sum is over all 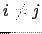 . If we analyze only the contribution of the spin i, we obtain that it is described by:
. If we analyze only the contribution of the spin i, we obtain that it is described by:
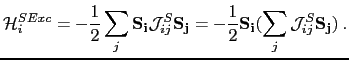 |
(138) |
In the case when the state of the system has the ferromagnetic order, where all the unit vectors
 are pointing out in the same direction, we can rewrite the last expression as:
are pointing out in the same direction, we can rewrite the last expression as:
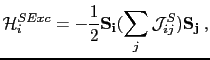 |
(139) |
being
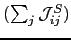 the effective symmetric contribution of the exchange interaction at layer
the effective symmetric contribution of the exchange interaction at layer 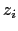 , it has been defined previously as
, it has been defined previously as
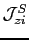 . As we have shown in the chapter 6.3.4, for Co(100) and
. As we have shown in the chapter 6.3.4, for Co(100) and
 the
the
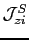 has the following form:
has the following form:
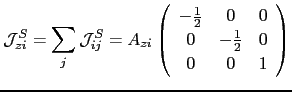 |
(140) |
This expression can be separated in two contributions,
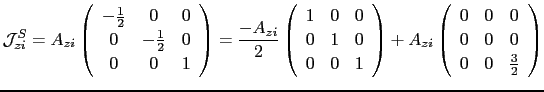 |
(141) |
Therefore we have that:
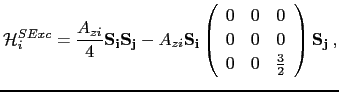 |
(142) |
This formula can be simplified as:
 |
(143) |
The first term on the right hand side (r.h.s) of this equation is isotropic and does not contribute to the anisotropy of the system, but it can modify the isotropic part of the exchange interaction. If we remember the initial hypothesis of the ferromagnetic state of the system, the second term in the (r.h.s.) of the equation A.19 can be expressed as:
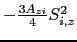 and this formula is analogous to that of the expression for the uniaxial anisotropy with easy axis parallel to the
and this formula is analogous to that of the expression for the uniaxial anisotropy with easy axis parallel to the 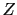 axis.
axis.
In conclusion the "two-site" anisotropy can contribute to the effective uniaxial anisotropy under the assumptions mentioned above.
Rocio Yanes
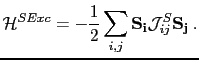
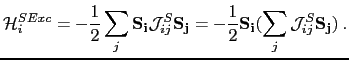
![]() are pointing out in the same direction, we can rewrite the last expression as:
are pointing out in the same direction, we can rewrite the last expression as: