Next: Bibliography Up: A. Appendix A Previous: 2 Contribution to total Contents
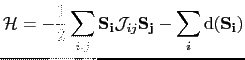 |
(144) |
In spherical coordinates we can write
![]() as a function of the polar and azimuthal angles
as a function of the polar and azimuthal angles
![]() and
and
![]() , respectively.
, respectively.
| (147) |
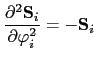 |
(150) |
Now we evaluate the second derivatives with respect to the polar and azimuthal angles of the energy:
 |
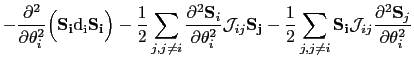 |
(151) | |
 |
 |
(152) |
Due to the fact that the spin variables are independent, the equations above can be reduced to:
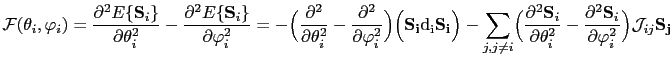 |
(155) |
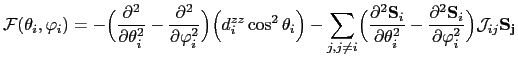 |
(156) |
Therefore we can calculate the on-site anisotropy constant
![]() evaluating the free energy at
evaluating the free energy at
![]()
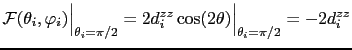 |
(157) |
with
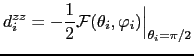 |
(158) |
Rocio Yanes