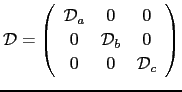Magnetostatic are other sources of the total magnetic anisotropy called the macroscopic shape anisotropy. This concept is clear in the case of homogeneous magnetization in a ellipsoid, where the demagnetization tensor can be introduced in such way that the demagnetization field can be defined as:
 |
(11) |
where
 is the demagnetization tensor,
is the demagnetization tensor,
 is the demagnetization field and
is the demagnetization field and
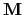 is the magnetization of the system. Thus the density magnetostatic energy can be described as:
is the magnetization of the system. Thus the density magnetostatic energy can be described as:
 |
(12) |
If the semiaxes a, b, and c of the ellipsoid represent the axes of the coordination system the
 is a diagonal tensor.
An arbitrary direction of the magnetization with respect to the semiaxes can
be characterized by the direction cosine
is a diagonal tensor.
An arbitrary direction of the magnetization with respect to the semiaxes can
be characterized by the direction cosine
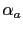 ,
,
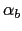 , and
, and
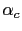 . The tensor is given
by:
. The tensor is given
by:
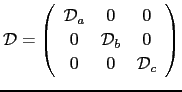 |
(13) |
and the magnetostatic energy density can be written as:
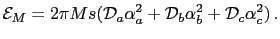 |
(14) |
For thin films, magnetostatic interaction leads to an additional anisotropy favoring the in-plane anisotropy. In the case of elongated nanoparticles, magnetostatic interactions produce an additional easy axis parallel to the long dimensions.
Rocio Yanes