It is known that the magnetization
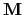 tends to orient preferentially along one or several axes in magnetic solids. The magnetic anisotropy energy is defined as the energy term that describes the dependence of the internal energy on the direction of the magnetization, and it may be originated by the crystalline electric field of the solid, by the shape or surface of the magnetic body, by mechanical stress etc.
Usually the magnetic anisotropy energy has the symmetry of the crystal structure of the material and it is invariant to the inversion of the magnetization. These facts mean that the magnetic anisotropy energy must be an expansion of even functions of the angles enclosed by the magnetization and the magnetic axes.
Hereafter we present the expressions of the magnetic anisotropy energy density (
tends to orient preferentially along one or several axes in magnetic solids. The magnetic anisotropy energy is defined as the energy term that describes the dependence of the internal energy on the direction of the magnetization, and it may be originated by the crystalline electric field of the solid, by the shape or surface of the magnetic body, by mechanical stress etc.
Usually the magnetic anisotropy energy has the symmetry of the crystal structure of the material and it is invariant to the inversion of the magnetization. These facts mean that the magnetic anisotropy energy must be an expansion of even functions of the angles enclosed by the magnetization and the magnetic axes.
Hereafter we present the expressions of the magnetic anisotropy energy density (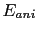 ) for the most frequent cases:
) for the most frequent cases:
- Cubic symmetry
- We denote
 as the cosines of the angles between the magnetization and the axes X;Y;Z parallel to the fourfold axes. Then
as the cosines of the angles between the magnetization and the axes X;Y;Z parallel to the fourfold axes. Then 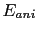 has the following form:
has the following form:
 |
(1) |
- Tetragonal symmetry
- If we denote
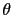 and
and 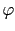 as the angles in polar coordinates, and Z as the axis parallel to the sixfold axis [001], then
as the angles in polar coordinates, and Z as the axis parallel to the sixfold axis [001], then 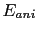 has the following form:
has the following form:
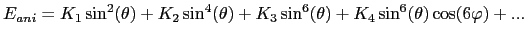 |
(2) |
- Quadratic symmetry
- In this symmetry there is a fourfold axis
![$ [001]$](img155.gif) , and Z is the axis parallel to that axis. Then
, and Z is the axis parallel to that axis. Then 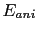 has the following form:
has the following form:
 |
(3) |
- Uniaxial symmetry
- The first terms in the expansion of
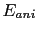 in the case of the tetragonal, rhombohedral and quadratic symmetries are the same. Usually the next term in the expansion is at least one order of magnitude smaller. Then if we restrict the expansion to the first term, we obtain that
in the case of the tetragonal, rhombohedral and quadratic symmetries are the same. Usually the next term in the expansion is at least one order of magnitude smaller. Then if we restrict the expansion to the first term, we obtain that 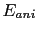 is of the second order and only depends on the angle between the magnetic moment and the axis of the highest symmetry
is of the second order and only depends on the angle between the magnetic moment and the axis of the highest symmetry 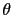 , in the following form:
, in the following form:
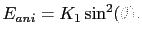 |
(4) |
This kind of magnetic anisotropy can also be found in amorphous material submitted to stress or isotropic magnetic material annealed under the presence of a magnetic field.
The values above
![$ [K_{i} (i=1,2,3,4...)]$](img158.gif) are the anisotropy constants with dimension [energy/volume]. These parameters depend on the temperature and material and they can range from around
are the anisotropy constants with dimension [energy/volume]. These parameters depend on the temperature and material and they can range from around
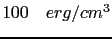 in soft materials, passing through
in soft materials, passing through
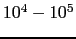
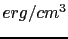 for 3d metals of cubic symmetry like Ni, Fe, etc., to
for 3d metals of cubic symmetry like Ni, Fe, etc., to
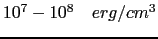 in some rare earth alloys and
in some rare earth alloys and 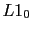 compound such as FePt and CoPt.
In practice,
compound such as FePt and CoPt.
In practice, 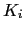 is usually derived from experiments (ferromagnetic resonance, magnetization curve, etc) as an empirical constant.
is usually derived from experiments (ferromagnetic resonance, magnetization curve, etc) as an empirical constant.
The total magnetic anisotropy can be the result of several contributions: the magneto-crystalline anisotropy (MCA), surface anisotropy, shape anisotropy, magnetostriction anisotropy, exchange anisotropy etc.
Subsections
Rocio Yanes