Magneto-crystalline anisotropy (MCA) is one of the most important energy contributions in magnetic materials and it is generated by the atomic structure and bonding in the magnetic material. Attempts to understand its microscopic origin have been taking place since many years ago. As proposed by Van Vleck [42], the origin to the MCA energy is the spin-orbit coupling interaction (SOC), which is the term that links the spatial and spin parts of the wave functions. In the case of a central potential 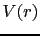 , its interaction is given as:
, its interaction is given as:
where 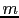 is the mass of the electron,
is the mass of the electron, 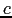 is the speed of light in the vacuum,
is the speed of light in the vacuum, 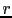 is the distance from the nuclei,
is the distance from the nuclei,
 and
and
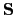 are orbital and spin moments.
We would like to note that this form of the SOC term has been used in almost all cases. Although the potential (
are orbital and spin moments.
We would like to note that this form of the SOC term has been used in almost all cases. Although the potential (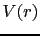 ) is not generally central, nevertheless as
) is not generally central, nevertheless as
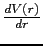 has its maxim contribution close to the nuclei, where
has its maxim contribution close to the nuclei, where 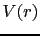 is approximated as the central potential, thus the approximation of SOC (1.5) is generally accepted.
is approximated as the central potential, thus the approximation of SOC (1.5) is generally accepted.
Theoretically the magneto-crystalline anisotropy is determined from the evaluation of the difference of the system's energy when the magnetization is orientated along the easy and hard axes. If other contributions such as the magnetostatic energy can be neglected, then the MCA is given by the anisotropy due to the spin-orbit coupling:
![$\displaystyle \Delta E_{SO}=\langle\mathcal{H}_{SO}\rangle_{hard}-\langle\mathc...
...dot \mathbf{S}\rangle_{hard}-\langle\mathbf{L}\cdot \mathbf{S}\rangle_{easy}]>0$](img176.gif) |
(7) |
where
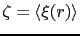 is the spin-orbit coupling constant.
This way the magnetization of the system in the hard direction requires an input of energy into the system.
The principal difficulty in the study of the MCA is its small size, for example in transition metals MCA is of the order of
is the spin-orbit coupling constant.
This way the magnetization of the system in the hard direction requires an input of energy into the system.
The principal difficulty in the study of the MCA is its small size, for example in transition metals MCA is of the order of 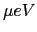 , which is usually in the limit of accuracy of theoretical calculations.
, which is usually in the limit of accuracy of theoretical calculations.
Rocio Yanes