1 Shape and surface of nanoparticles

In this study we show that the magnetic behavior of small particles is very sensitive to the surface arrangement, shape of the particles and underlying crystallographic structure. To investigate the various tendencies, we have considered particles cut from lattices with the simple cubic (sc) and face-centered cubic (fcc).

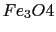Figure 2.1: Image TEM of magnetic nanoparticles: (left) nanoparticles of $\gamma -Fe_{2}O_{3}$ (from Ref.[88]) and (right) azide functionalized $Fe_{3}O{4}$ nanoparticles (right) (from Ref. [89]).

Although experimental studies providing transmission electron microscopy images often show particles resembling truncated octahedra [20,14] ( see Figs. 1.1 in section 1.1 of the chapter Introduction). The real particles are not regular see for example Fig. 2.1, where we can find TEM images of different kind of nanoparticles. Making realistic particle shapes and surface arrangements in a computer simulations proves to be rather complex, "ab-initio" simulations are available only for small clusters [72,71]. Truncated octahedra have been included in our studies as an ideal case for fcc crystals, but the reality is somewhat subtler. In Ref. [14], in order to interpret the experimental results of the $3D$-dimensional switching field curve, the so called Stoner-Wohlfarth astroid, it was assumed that a few outer layers in the truncated octahedral particle were magnetically ``dead", leading to an effective elongation and thereby to a non-perfect octahedron. Producing such a faceted elongated particle by somehow cutting the latter is an arbitrary procedure. In order to minimize the changes in the surface structure caused by elongation, we assumed a spherical particle or introduced elliptical elongation along the easy axis. This kind of structure has been the basis of many theoretical studies using the Heisenberg Hamiltonian (see, e.g., Refs. [90,91,92,74,75,87,93,94]).

Figure 2.2: Two particles cut from fcc structure: spherical (left) and truncated octahedron (right).

Regarding the arrangement on the particle's surface, an appropriate approach would be to use molecular-dynamic techniques [95,84,96] based on the empirical potentials for specific materials. This would produce more realistic non-perfect surface structures, more representative of what it is hinted to experimentally. However, these potentials exist only for some specific materials and do not fully include the complex character of the surface. Moreover, the particles thus obtained (see, e.g. Ref. [18]), may have non-symmetric structures, and may present some dislocations. All these phenomena lead to rich and different behavior of differently prepared particles.

In the present chapter, and in order to illustrate the general tendency of the magnetic behavior, we mostly present results for particles with "pure" non-modified surfaces, namely spheres, ellipsoids and truncated octahedra cut from regular lattices. Even in this case, the surface arrangement may appears to be very different (see Fig. 2.2) leading to a rich magnetic behavior.