Next: 3 Analytical background Up: 2 Model Previous: 1 Shape and surface Contents
The anisotropy energy
![]() will be different if we are working with core spins or surface spins. For core spins, i.e., those spins with full coordination, the
anisotropy energy
will be different if we are working with core spins or surface spins. For core spins, i.e., those spins with full coordination, the
anisotropy energy
![]() is taken either as
uniaxial with easy axis along
is taken either as
uniaxial with easy axis along ![]() and a constant
and a constant ![]() (per
atom), that is
(per
atom), that is
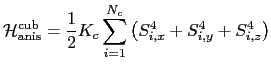 |
(20) |
Dipolar interactions are known to produce an additional "shape" anisotropy. However, in the atomistic description, their role in describing the spin non-collinearities is negligible as compared to that of all other contributions. In order to compare particles with the same strength of anisotropy in the core, we assume that the shape anisotropy is included in the core uniaxial anisotropy and neglect the dipolar energy contribution to the spin non-collinearities. We also assume that in the ellipsoidal nanoparticles the anisotropy easy axis is parallel to the elongation direction.
All physical constants will be measured with respect to the
exchange coupling ![]() (unless explicitly stated otherwise), so we define the reduced constants,
(unless explicitly stated otherwise), so we define the reduced constants,
| (22) |
Rocio Yanes