3 Analytical background
In Refs. [74,87,97,73]
analytical as well as numerical calculations showed that a
multi-spin particle, cut from a sc lattice, and when its surface
anisotropy is small with respect to the exchange coupling,
may be modeled by an effective one-spin particle (EOSP), i.e., a
single macroscopic magnetic moment
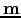 representing the net
magnetic moment of the multi-spin particle. The energy of this EOSP
(normalized to
representing the net
magnetic moment of the multi-spin particle. The energy of this EOSP
(normalized to  ) may be written as
) may be written as
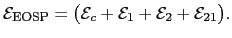 |
(23) |
The
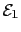 is the first-order anisotropy energy with surface contribution,
is the first-order anisotropy energy with surface contribution,
 is the second-order anisotropy energy with surface contribution,
is the second-order anisotropy energy with surface contribution,
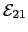 is a mixed contribution to the energy that is second order in surface anisotropy and first order in core anisotropy and
is a mixed contribution to the energy that is second order in surface anisotropy and first order in core anisotropy and
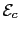 is the core anisotropy energy (per spin).
is the core anisotropy energy (per spin).
The
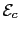 energy has the following form:
energy has the following form:
 |
(24) |
The other three contributions (
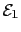 ,
,
 and
and
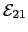 ) stem from the surface, which we discuss now.
) stem from the surface, which we discuss now.
Subsections
Rocio Yanes
![]() energy has the following form:
energy has the following form:

![]() ,
,
![]() and
and
![]() ) stem from the surface, which we discuss now.
) stem from the surface, which we discuss now.