In Ref. [74] the case of non-symmetrical particles was also discussed. More precisely, for small deviations from spheres and cubes, i.e., for weakly ellipsoidal or weakly rectangular particles, there is a corresponding weak first-order contribution
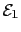 that adds up to
that adds up to
 .
Hence, for an ellipsoid of revolution with axes
.
Hence, for an ellipsoid of revolution with axes 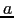 and
and
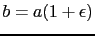 ,
,
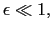 cut out of an sc lattice so that the ellipsoid's axes are parallel to the crystallographic direction, one has that the first order anisotropy is given by [97]:
cut out of an sc lattice so that the ellipsoid's axes are parallel to the crystallographic direction, one has that the first order anisotropy is given by [97]:
 |
(33) |
where
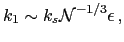 |
(34) |
i.e. the
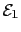 energy contribution scales with the surface of the system.
energy contribution scales with the surface of the system.
It is necessary to mention that for crystal shapes such as spheres and cubes the contribution
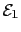 vanishes by symmetry.
vanishes by symmetry.
The ratio of the second to the first order surface contributions is:
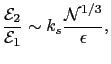 |
(35) |
It can be significant even for
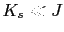 due to the combined influence of the large particle size and the small deviation from symmetry,
due to the combined influence of the large particle size and the small deviation from symmetry,
 .
Rocio Yanes
.
Rocio Yanes
![]() vanishes by symmetry.
vanishes by symmetry.