4 Numerical method
Since we are dealing with a multi-spin particle, the energy
potential is multidimensional. Accordingly, in Ref. [74] the technique of
Lagrange multiplier was introduced to represent the energy
potential in terms of the coordinates of the particle's net
magnetization
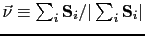 .
This technique consists of adding the term
.
This technique consists of adding the term
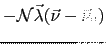 , to the total energy Eq. (2.1).
This term produces an additional torque that forces the net
magnetization to lie along the prescribed direction
, to the total energy Eq. (2.1).
This term produces an additional torque that forces the net
magnetization to lie along the prescribed direction
 .
The equilibrium state of the spin system is determined by solving
the Landau-Lifshitz equation (without the precession term):
.
The equilibrium state of the spin system is determined by solving
the Landau-Lifshitz equation (without the precession term):
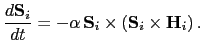 |
(41) |
The effective field
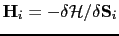 now contains an additional term due to the Lagrange
constraint.
For the three components of the Lagrange parameter
now contains an additional term due to the Lagrange
constraint.
For the three components of the Lagrange parameter
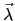 the set of equations (2.24) is augmented by the equations
the set of equations (2.24) is augmented by the equations
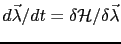 .
The stationary points found with this method are also stationary
points of the Hamiltonian (2.1), since for these
points
.
The stationary points found with this method are also stationary
points of the Hamiltonian (2.1), since for these
points
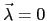 . However, if the system has many
metastable states, only part of these points, compatible with the
behavior assumed by the direction of the net magnetization is
determined. More precisely, in individual small particles where
the exchange interaction is dominating, the deviations from the
collinear state are small and thereby the individual spins
adiabatically adjust to the net direction when the latter is
rotated. In this case, it is possible to define a net
magnetization and parameterize it, e.g., in the spherical system
of coordinates as
. However, if the system has many
metastable states, only part of these points, compatible with the
behavior assumed by the direction of the net magnetization is
determined. More precisely, in individual small particles where
the exchange interaction is dominating, the deviations from the
collinear state are small and thereby the individual spins
adiabatically adjust to the net direction when the latter is
rotated. In this case, it is possible to define a net
magnetization and parameterize it, e.g., in the spherical system
of coordinates as
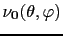 .
The advantage of this technique is that it can produce highly non-collinear multi-dimensional stationary points [74,87,99]. Accordingly, in the present work and unlike the studies presented in Ref. [14], spin non-collinearities are taken into account. Moreover, in order to check the correct loci of the saddle points, we computed the eigenvalues and gradient of the Hessian matrix associated with the Hamiltonian (2.1).
.
The advantage of this technique is that it can produce highly non-collinear multi-dimensional stationary points [74,87,99]. Accordingly, in the present work and unlike the studies presented in Ref. [14], spin non-collinearities are taken into account. Moreover, in order to check the correct loci of the saddle points, we computed the eigenvalues and gradient of the Hessian matrix associated with the Hamiltonian (2.1).
Rocio Yanes