3 Temperature dependence of the bulk anisotropy
Next we check well known results for the low temperature dependence of the bulk anisotropy, as predicted
by Callen and Callen theory in Refs. [106,129],
Figure 4.4:
Temperature dependence of magnetization, macroscopic uniaxial
and cubic anisotropies, for a ferromagnetic material with  spins and a simple cubic lattice with periodic boundary conditions in
spins and a simple cubic lattice with periodic boundary conditions in 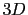 .
.
|
|
where uniaxial anisotropy was shown
to have an  dependence, and cubic anisotropy to have an
dependence, and cubic anisotropy to have an
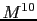 dependence. In the constrained Monte Carlo method we evaluate the torque curves at different temperatures from which we extract the value of the macroscopic anisotropy constant at different temperatures.
dependence. In the constrained Monte Carlo method we evaluate the torque curves at different temperatures from which we extract the value of the macroscopic anisotropy constant at different temperatures.
Figure 4.5:
Temperature scaling of the anisotropy versus magnetization of a ferromagnetic material with  moments, a simple cubic lattice, uniaxial anisotropy and periodic boundary conditions in
moments, a simple cubic lattice, uniaxial anisotropy and periodic boundary conditions in 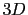 , for the whole temperature range (Left) and the fitting at low-temperatures (Right).
, for the whole temperature range (Left) and the fitting at low-temperatures (Right).
![\includegraphics[totalheight=0.27\textheight]{LD_sc_uni_ganmaT.eps}](img658.gif)
![\includegraphics[totalheight=0.27\textheight]{Ganma_uni.eps}](img659.gif) |
We simulate a generic ferromagnetic material with 1000 spins, simple cubic crystalline structure, the magnetic parameters are those exposed in Tab 4.1. We analyze both cases of uniaxial and cubic anisotropy and the "on-site" anisotropy constant values are the same for both cases. We also consider periodic boundary conditions in 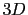 .
.
The magnetization and macroscopic uniaxial and cubic anisotropy are plotted
against temperature in Fig. 4.4. We can observe that the cubic anisotropy constant has a more pronounced dependence on temperature than the uniaxial one.
Figure 4.6:
Temperature scaling of the effective anisotropy versus magnetization of a ferromagnetic material with a simple cubic lattice,  moments, cubic anisotropy and periodic boundary conditions in
moments, cubic anisotropy and periodic boundary conditions in 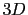 , for the whole temperature range (Left), and the fitting at low-temperatures (Right).
, for the whole temperature range (Left), and the fitting at low-temperatures (Right).
![\includegraphics[totalheight=0.27\textheight]{GamT_LD_sc_cub_Bulk.eps}](img660.gif)
![\includegraphics[totalheight=0.27\textheight]{Ganma_LD_sc_cub_Bulk.eps}](img661.gif) |
Figure 4.7:
Low-temperatures scaling of the effective anisotropy versus magnetization of a pure ferromagnet (with  moments) with fcc structure, periodic boundary conditions in
moments) with fcc structure, periodic boundary conditions in 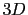 with uniaxial anisotropy (left) and cubic anisotropy (right).
with uniaxial anisotropy (left) and cubic anisotropy (right).
![\includegraphics[totalheight=0.27\textheight]{Ganma_LD_fcc_uni_Bulk.eps}](img662.gif)
![\includegraphics[totalheight=0.27\textheight]{Ganma_fcc_cub_Bulk.eps}](img663.gif)
|
In Figs. 4.5 and 4.6 the macroscopic anisotropies are plotted
against the magnetization on logarithmic scales. In this way we can extract the scaling exponent 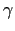 (
(
 ) at low-temperatures.
As it can be seen, the results are consistent with the scaling behavior predicted
by Callen and Callen [106]. Namely, in the system with uniaxial anisotropy we found
) at low-temperatures.
As it can be seen, the results are consistent with the scaling behavior predicted
by Callen and Callen [106]. Namely, in the system with uniaxial anisotropy we found
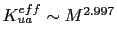 ( see Fig. 4.5) and for the cubic anisotropy case
( see Fig. 4.5) and for the cubic anisotropy case
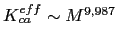 (see Fig. 4.6) at low temperatures.
(see Fig. 4.6) at low temperatures.
Next we simulate a generic ferromagnetic material with fcc crystalline structure with periodic boundary conditions in  . The magnetic parameters of the system are again those shown in the Tab. 4.1 and we investigate the cases of uniaxial and cubic magneto-crystalline anisotropy.
For uniaxial anisotropy we found that
. The magnetic parameters of the system are again those shown in the Tab. 4.1 and we investigate the cases of uniaxial and cubic magneto-crystalline anisotropy.
For uniaxial anisotropy we found that
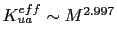 (see Fig. 4.7 left) and for cubic anisotropy
(see Fig. 4.7 left) and for cubic anisotropy
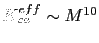 , at low temperatures ( see Fig. 4.7 right).
, at low temperatures ( see Fig. 4.7 right).
Given the results we can say that the behavior of the macroscopic anisotropy at low temperatures, obtained by the CMC method, corresponds with the predicted by Callen and Callen, both in the cases of sc and fcc lattices.
Rocio Yanes
![\includegraphics[totalheight=0.35\textheight]{KT_MT_LD_uni_cub.eps}](img655.gif)
![\includegraphics[totalheight=0.27\textheight]{LD_sc_uni_ganmaT.eps}](img658.gif)
![\includegraphics[totalheight=0.27\textheight]{Ganma_uni.eps}](img659.gif)
![\includegraphics[totalheight=0.27\textheight]{GamT_LD_sc_cub_Bulk.eps}](img660.gif)
![\includegraphics[totalheight=0.27\textheight]{Ganma_LD_sc_cub_Bulk.eps}](img661.gif)
![\includegraphics[totalheight=0.27\textheight]{Ganma_LD_fcc_uni_Bulk.eps}](img662.gif)
![\includegraphics[totalheight=0.27\textheight]{Ganma_fcc_cub_Bulk.eps}](img663.gif)
![]() . The magnetic parameters of the system are again those shown in the Tab. 4.1 and we investigate the cases of uniaxial and cubic magneto-crystalline anisotropy.
For uniaxial anisotropy we found that
. The magnetic parameters of the system are again those shown in the Tab. 4.1 and we investigate the cases of uniaxial and cubic magneto-crystalline anisotropy.
For uniaxial anisotropy we found that
![]() (see Fig. 4.7 left) and for cubic anisotropy
(see Fig. 4.7 left) and for cubic anisotropy
![]() , at low temperatures ( see Fig. 4.7 right).
, at low temperatures ( see Fig. 4.7 right).