5 On the applicability of the formula

The results presented above show that in the most general case,
studied here, of a multi-spin particle with Néel surface
anisotropy, this formula is not applicable, for the following
reasons:
- (i)
- It assumes that the overall anisotropy of the particle remains uniaxial. However, we have shown that the surface anisotropy induces an additional cubic contribution.
- (ii)
- It assumes that the surface anisotropy always enhances that in the core. In this and the previous sections we saw that both situations can arise.
- (iii)
- It is implicitly based on the hypothesis that the core and surface anisotropies are additive contributions. As we have seen above for large
 the energy barrier indeed can be represented as a sum of the effective cubic and uniaxial anisotropies. However, the cubic anisotropy term is proportional to
the energy barrier indeed can be represented as a sum of the effective cubic and uniaxial anisotropies. However, the cubic anisotropy term is proportional to 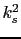 , which is inconsistent with formula (3.5).
, which is inconsistent with formula (3.5).
- (iv)
- It assumes linear dependence of energy barriers on the parameter
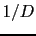 , or equivalently
, or equivalently
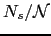 .
.
Consequently, spherical or octahedral particles cannot be described by formula (3.5), since in this case:
- (i)
- No term linear in
 is obtained.
is obtained.
- (ii)
- No term scales as the ratio of the surface-to-volume number of spins
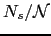 .
.
However, in the case of elongated particles with a not too large
surface anisotropy, i.e.,
 , the energy barriers are
independent of the effective cubic anisotropy. In this case, for
weakly ellipsoidal particles, for example, we may write
, the energy barriers are
independent of the effective cubic anisotropy. In this case, for
weakly ellipsoidal particles, for example, we may write
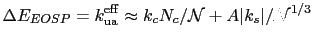 |
(52) |
where 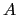 is a parameter that depends on the particle's elongation and surface arrangement, and which is positive for
is a parameter that depends on the particle's elongation and surface arrangement, and which is positive for 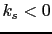 and
negative in the opposite case.
Hence, the behavior is as predicted by this formula (3.5). The approximately linear behavior in
and
negative in the opposite case.
Hence, the behavior is as predicted by this formula (3.5). The approximately linear behavior in
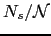 was also observed in the case of large surface anisotropy
was also observed in the case of large surface anisotropy 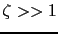 (see Fig. 3.1). However, in this case at
(see Fig. 3.1). However, in this case at
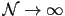 , the ``uniaxial anisotropy term"
, the ``uniaxial anisotropy term"
 is renormalized by the effective cubic anisotropy
is renormalized by the effective cubic anisotropy
 .
In Fig. 3.8 we plot the energy barriers of small
ellipsoidal particles with sc structure, aspect ratio 2:3, and
.
In Fig. 3.8 we plot the energy barriers of small
ellipsoidal particles with sc structure, aspect ratio 2:3, and
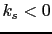 from Fig. 3.7.
from Fig. 3.7.
Figure 3.8:
Linear fit of energy barriers, versus the ratio of the surface-to-total number of spins
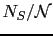 , of ellipsoidal particles with aspect ratio 2:3 with
, of ellipsoidal particles with aspect ratio 2:3 with
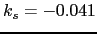 (circles) and
(circles) and
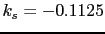 (squares).
(squares).
|
|
For such particles, the formula (3.5) should be modified as
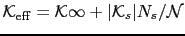 . Accordingly, in Fig. 3.8 we plot the energy barrier against
. Accordingly, in Fig. 3.8 we plot the energy barrier against
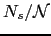 . These data are well fitted to straight lines, especially when small particle sizes are removed. We note that in the case of relatively small surface anisotropy
. These data are well fitted to straight lines, especially when small particle sizes are removed. We note that in the case of relatively small surface anisotropy
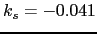 (though 17 times larger than that in the core), the full core anisotropy
(though 17 times larger than that in the core), the full core anisotropy
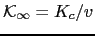 (
(  is the atomic volume) can be extracted. However, for the larger surface anisotropy
is the atomic volume) can be extracted. However, for the larger surface anisotropy
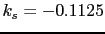 ,
,
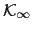 is renormalized by the surface contribution, defined by Eq. (2.15). On the other hand, it is not possible to extract the value of
is renormalized by the surface contribution, defined by Eq. (2.15). On the other hand, it is not possible to extract the value of  , since the exact proportionality coefficient of Eq. (2.17) (the value of A in Eq. 3.10) is dependent on the particles surface arrangement and elongation.
The effective anisotropy constant
, since the exact proportionality coefficient of Eq. (2.17) (the value of A in Eq. 3.10) is dependent on the particles surface arrangement and elongation.
The effective anisotropy constant
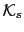 obtained from this fit is much smaller than the input value, namely, for
obtained from this fit is much smaller than the input value, namely, for
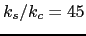 we obtain from the fit
we obtain from the fit
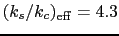 .
Rocio Yanes
.
Rocio Yanes
![\includegraphics[totalheight=0.35\textheight]{barrier_ellips_1.eps}](img506.gif)