As we have shown in the previous chapter, the numerical evaluation of the energy barrier should be done in a multidimensional space and it is a difficult task. With this aim we use the Lagrange-multiplier method described in section 2.4. We evaluate the energy barriers of multi-spin particles (MSPs) by numerically
computing the difference between the energy at the saddle point
and at the minimum, and compare them with analytical results obtained from the EOSP approximation.
Note that in the wide range of the parameters several energy
barriers (corresponding to different paths of magnetization
rotation) coexist in the system in accordance with the complex
character of the effective potential with two competitive
anisotropies, see Figs. 2.3(c) and
2.9(c). In what follows, in most cases we
will only discuss the energy barrier which corresponds to the
change in 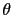 direction. In the case corresponding to elongated nanoparticles cut from fcc lattice and uniaxial anisotropy in the core, see
Fig.2.9(d), the only energy barrier
corresponds to the rotation around
direction. In the case corresponding to elongated nanoparticles cut from fcc lattice and uniaxial anisotropy in the core, see
Fig.2.9(d), the only energy barrier
corresponds to the rotation around 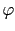 direction.
direction.
Figure 3.2:
Energy barrier as a function of  for a spherical
particle cut from an sc lattice. The particle contains
for a spherical
particle cut from an sc lattice. The particle contains
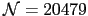 spins and has the uniaxial core anisotropy
spins and has the uniaxial core anisotropy
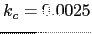 .
The solid line is a plot of the analytical expression
(3.8).
.
The solid line is a plot of the analytical expression
(3.8).
|
|
Figure 3.3:
Energy barriers against  for truncated octahedral multi-spin particle cut from an fcc lattice (
for truncated octahedral multi-spin particle cut from an fcc lattice (
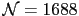 ) and spherical particles cut from the fcc (
) and spherical particles cut from the fcc (
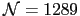 ) and hcp (
) and hcp (
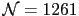 ) lattices. Uniaxial core anisotropy with
) lattices. Uniaxial core anisotropy with
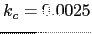 is assumed.
is assumed.
|
|
Fig. 3.2 shows the energy barrier of a spherical
particle cut from an sc lattice as a function of  . The
nonlinear behavior of the energy barrier with
. The
nonlinear behavior of the energy barrier with  follows
quantitatively that of the EOSP potential (3.7).
Indeed, the solid line in this plot is the analytical result
(3.8), using analytical expressions of Eqs. (2.14-2.15) together
with the pure core anisotropy contribution.
The discrepancy at the relatively large
follows
quantitatively that of the EOSP potential (3.7).
Indeed, the solid line in this plot is the analytical result
(3.8), using analytical expressions of Eqs. (2.14-2.15) together
with the pure core anisotropy contribution.
The discrepancy at the relatively large  is due to the fact that the analytical expressions are valid only if the condition (2.22) is fulfilled; the core-surface mixing (CSM) contribution has not been taken into account.
is due to the fact that the analytical expressions are valid only if the condition (2.22) is fulfilled; the core-surface mixing (CSM) contribution has not been taken into account.
In Fig. 3.3 we represent the energy barriers as a function of  for MSPs with different shapes and internal structures. First of
all, one can see a different dependence on
for MSPs with different shapes and internal structures. First of
all, one can see a different dependence on  as compared to
MSPs with the sc lattice. In the present case, i.e.,
as compared to
MSPs with the sc lattice. In the present case, i.e.,
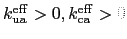 , the
energy barriers are given by
Eqs. (3.9)(a) and (c).
For small values of
, the
energy barriers are given by
Eqs. (3.9)(a) and (c).
For small values of  , for which
, for which
 ,
the energy barrier, in the first approximation neglecting the CSM
term, is independent of
,
the energy barrier, in the first approximation neglecting the CSM
term, is independent of  . Accordingly, the nearly constant
value of the energy barrier, coinciding with that of the core, is
observed for multi-spin particles in a large range of
. Accordingly, the nearly constant
value of the energy barrier, coinciding with that of the core, is
observed for multi-spin particles in a large range of  .
For larger
.
For larger  , the energy barrier increases, since
, the energy barrier increases, since
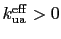 for
multi-spin particles cut from an fcc lattice. At very large values of
for
multi-spin particles cut from an fcc lattice. At very large values of  , i.e.,
, i.e.,
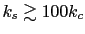 the energy barriers depend approximately linearly on
the energy barriers depend approximately linearly on  and may have
values larger than that inferred from the pure core anisotropy.
and may have
values larger than that inferred from the pure core anisotropy.
The energy barriers for ellipsoidal multi-spin particles are shown in Fig. 3.4.
Figure 3.4:
Energy barriers versus  of ellipsoidal multi-spin particles with different aspect ratio (
of ellipsoidal multi-spin particles with different aspect ratio (
 , and
, and
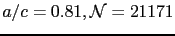 , with uniaxial core anisotropy
, with uniaxial core anisotropy
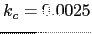 . The solid lines are linear fits.
. The solid lines are linear fits.
|
|
Note that in this case the effective uniaxial anisotropy constant
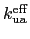 is a linear function of
is a linear function of  , according to the analytical results (2.16), (2.17) and the numerical results presented in
Fig. 2.10.
In this case the value of the energy barrier is not symmetric with respect to the change of the sign of
, according to the analytical results (2.16), (2.17) and the numerical results presented in
Fig. 2.10.
In this case the value of the energy barrier is not symmetric with respect to the change of the sign of  . This is due to the fact that for
. This is due to the fact that for 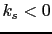 the effective uniaxial constant is a sum of the core anisotropy and the first-order contribution owing to elongation. On the contrary, when
the effective uniaxial constant is a sum of the core anisotropy and the first-order contribution owing to elongation. On the contrary, when 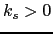 , the "effective core anisotropy"
, the "effective core anisotropy"
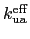 is smaller than the pure core anisotropy
is smaller than the pure core anisotropy
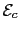 in Eq. (2.6).
This means that at some
in Eq. (2.6).
This means that at some  the effective uniaxial anisotropy constant (
the effective uniaxial anisotropy constant (
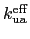 ) may change sign. At the same time the effective cubic anisotropy
) may change sign. At the same time the effective cubic anisotropy
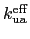 remains positive and is proportional to
remains positive and is proportional to 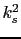 . Accordingly, at the vicinity of the point at which
. Accordingly, at the vicinity of the point at which
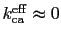 , rapid changes of the character of the energy landscape occur as we have shown in Fig. 2.10 in the previous chapter.
, rapid changes of the character of the energy landscape occur as we have shown in Fig. 2.10 in the previous chapter.
The analysis, based on the effective one spin problem potential shows that when
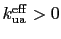 the energy barriers of ellipsoidal multi-spin particles are defined by Eqs. 3.9(a) and (c), and for negative
the energy barriers of ellipsoidal multi-spin particles are defined by Eqs. 3.9(a) and (c), and for negative
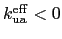 these are given by Eq. 3.9(b) and (c).
these are given by Eq. 3.9(b) and (c).
We would like to note that a regime of linear behavior in  exists for both
exists for both
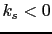 and
and 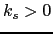 (see Fig. 3.4). In some region
of the effective anisotropy constants, e.g.,
(see Fig. 3.4). In some region
of the effective anisotropy constants, e.g.,
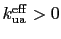 ,
,  , the energy barrier
, the energy barrier
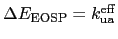 , i.e., it is
independent of the cubic contribution (neglecting again the CSM
term). Consequently, it is linear in
, i.e., it is
independent of the cubic contribution (neglecting again the CSM
term). Consequently, it is linear in  , according to
Eq. (2.17). The interval of these parameters is especially
large in MSPs with
, according to
Eq. (2.17). The interval of these parameters is especially
large in MSPs with 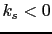 for which
for which
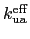 does not change sign.
does not change sign.
Rocio Yanes
![]() direction. In the case corresponding to elongated nanoparticles cut from fcc lattice and uniaxial anisotropy in the core, see
Fig.2.9(d), the only energy barrier
corresponds to the rotation around
direction. In the case corresponding to elongated nanoparticles cut from fcc lattice and uniaxial anisotropy in the core, see
Fig.2.9(d), the only energy barrier
corresponds to the rotation around ![]() direction.
direction.
![\includegraphics[totalheight=0.30\textheight]{deltaE_Co_Ks_2_2.eps}](img480.gif)
![\includegraphics[totalheight=0.30\textheight]{Bar_fcc_hcp_R.eps}](img481.gif)
![]() for MSPs with different shapes and internal structures. First of
all, one can see a different dependence on
for MSPs with different shapes and internal structures. First of
all, one can see a different dependence on ![]() as compared to
MSPs with the sc lattice. In the present case, i.e.,
as compared to
MSPs with the sc lattice. In the present case, i.e.,
![]() , the
energy barriers are given by
Eqs. (3.9)(a) and (c).
For small values of
, the
energy barriers are given by
Eqs. (3.9)(a) and (c).
For small values of ![]() , for which
, for which
![]() ,
the energy barrier, in the first approximation neglecting the CSM
term, is independent of
,
the energy barrier, in the first approximation neglecting the CSM
term, is independent of ![]() . Accordingly, the nearly constant
value of the energy barrier, coinciding with that of the core, is
observed for multi-spin particles in a large range of
. Accordingly, the nearly constant
value of the energy barrier, coinciding with that of the core, is
observed for multi-spin particles in a large range of ![]() .
For larger
.
For larger ![]() , the energy barrier increases, since
, the energy barrier increases, since
![]() for
multi-spin particles cut from an fcc lattice. At very large values of
for
multi-spin particles cut from an fcc lattice. At very large values of ![]() , i.e.,
, i.e.,
![]() the energy barriers depend approximately linearly on
the energy barriers depend approximately linearly on ![]() and may have
values larger than that inferred from the pure core anisotropy.
and may have
values larger than that inferred from the pure core anisotropy.
![\includegraphics[totalheight=0.35\textheight]{deltaE_Co_Ks_ellip.eps}](img484.gif)
![]() the energy barriers of ellipsoidal multi-spin particles are defined by Eqs. 3.9(a) and (c), and for negative
the energy barriers of ellipsoidal multi-spin particles are defined by Eqs. 3.9(a) and (c), and for negative
![]() these are given by Eq. 3.9(b) and (c).
these are given by Eq. 3.9(b) and (c).
![]() exists for both
exists for both
![]() and
and ![]() (see Fig. 3.4). In some region
of the effective anisotropy constants, e.g.,
(see Fig. 3.4). In some region
of the effective anisotropy constants, e.g.,
![]() ,
, ![]() , the energy barrier
, the energy barrier
![]() , i.e., it is
independent of the cubic contribution (neglecting again the CSM
term). Consequently, it is linear in
, i.e., it is
independent of the cubic contribution (neglecting again the CSM
term). Consequently, it is linear in ![]() , according to
Eq. (2.17). The interval of these parameters is especially
large in MSPs with
, according to
Eq. (2.17). The interval of these parameters is especially
large in MSPs with ![]() for which
for which
![]() does not change sign.
does not change sign.